主成次分析

机器学习
1.8k 词

基本假设和完全共线性（Perfect Multicollinearity）

多元线性回归模型中，数据矩阵（其中含有常数项列）被假设具有满列秩（full column rank），也就是说它的列向量线性无关。换言之，。

如果存在一个非零向量 ，使得


那么就意味着矩阵 的列是线性相关的，此时我们称 存在完全共线性（perfect multicollinearity）。

此时，不可逆，，因此我们无法通过正规方程

来估计参数。

近似共线性（Collinearity）

虽然真实数据中完全共线性是罕见的，但经常会出现“近似”共线性，即：

此时称为“多重共线性”或“近似共线性”。

虽然 的列仍然线性无关（即 ，但 非奇异矩阵的行列式很小（接近奇异），于是其逆矩阵 的元素就会很大.

对估计方差的影响

我们知道回归系数的协方差矩阵是：

当 的某些特征值接近 0，导致 某些对角线元素很大，从而导致某些参数估计的方差极大。

换句话说，如果你用回归模型去估计这些 ，会发现估计值对样本扰动非常敏感，标准误特别大，t检验显著性很低 —— 即模型回归整体有效（R²高），但每个变量看上去都“不显著”。

对称正半定矩阵

一个实对称矩阵 被称为对称正半定矩阵（symmetric positive semi-definite），如果满足：

并且 （即对称）

主成分分析 (Principal Component Analysis, PCA)

  • 目标： PCA的目标是找到数据中“方差最大”的方向，将高维数据投影到这些方向上（即主成分），从而在保留最多信息的前提下，实现数据降维和去相关性。

  • 传统实现方法：

    1. 数据中心化： 对数据的每一个特征（列），减去该特征的均值。
    2. 计算协方差矩阵： 计算中心化后数据矩阵的协方差矩阵。协方差矩阵描述了不同特征之间的线性关系。
    3. 特征值分解： 对协方差矩阵进行特征值分解，得到特征值（Eigenvalues）和对应的特征向量（Eigenvectors）。
    4. 选取主成分： 特征向量就是主成分的方向，而特征值的大小代表了数据在对应方向上的方差。选取最大的几个特征值对应的特征向量，就构成了新的低维空间。
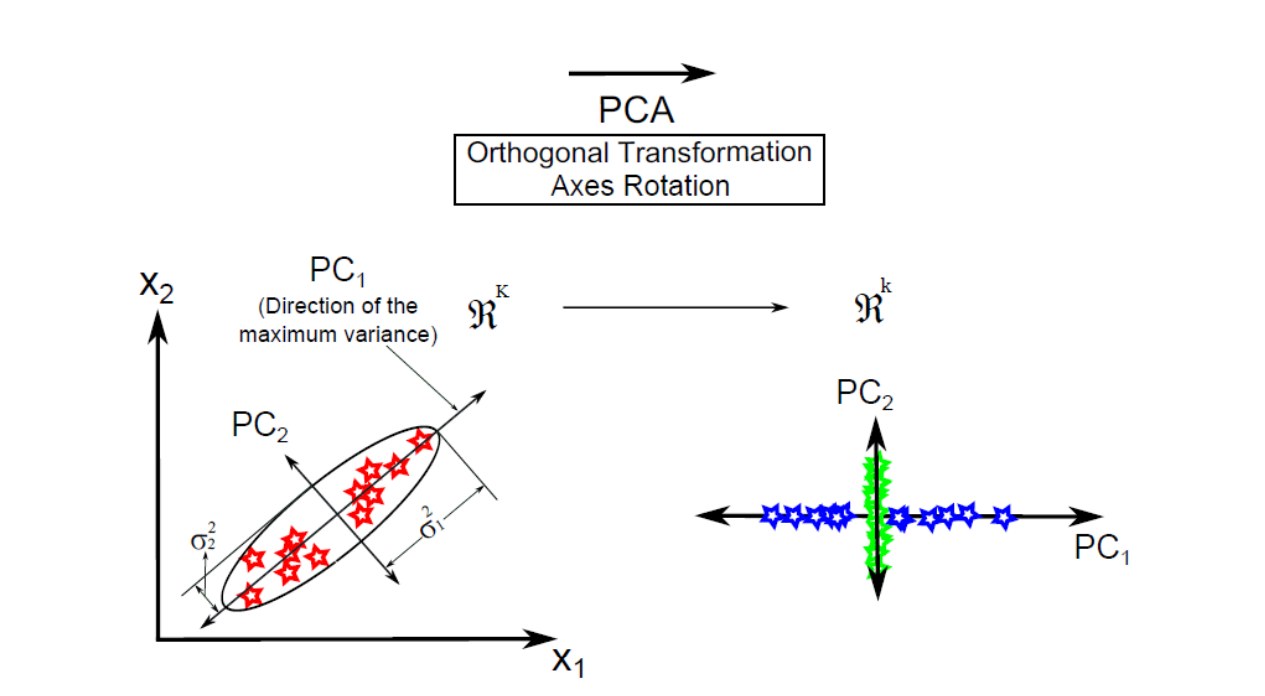
      image.png

主成分是如何选出的

线性变换定义

这部分定义了一个线性变换：

令 是原始变量向量，构造一个线性变换 ，得到新变量 。具体写法是：

也就是：，矩阵 。

主成分本质上就是一组新的坐标轴，每一条轴是原始变量的线性组合方向

用于后面推导主成分的最大方差方向

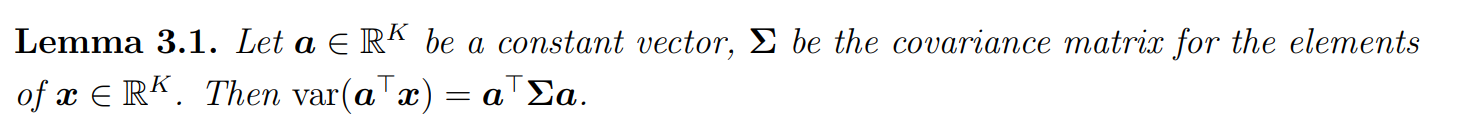
image.png

后续要对数据集X寻找最大方差使用这个lemma

PCA 三大原则

image.png

最大方差和第一主成分

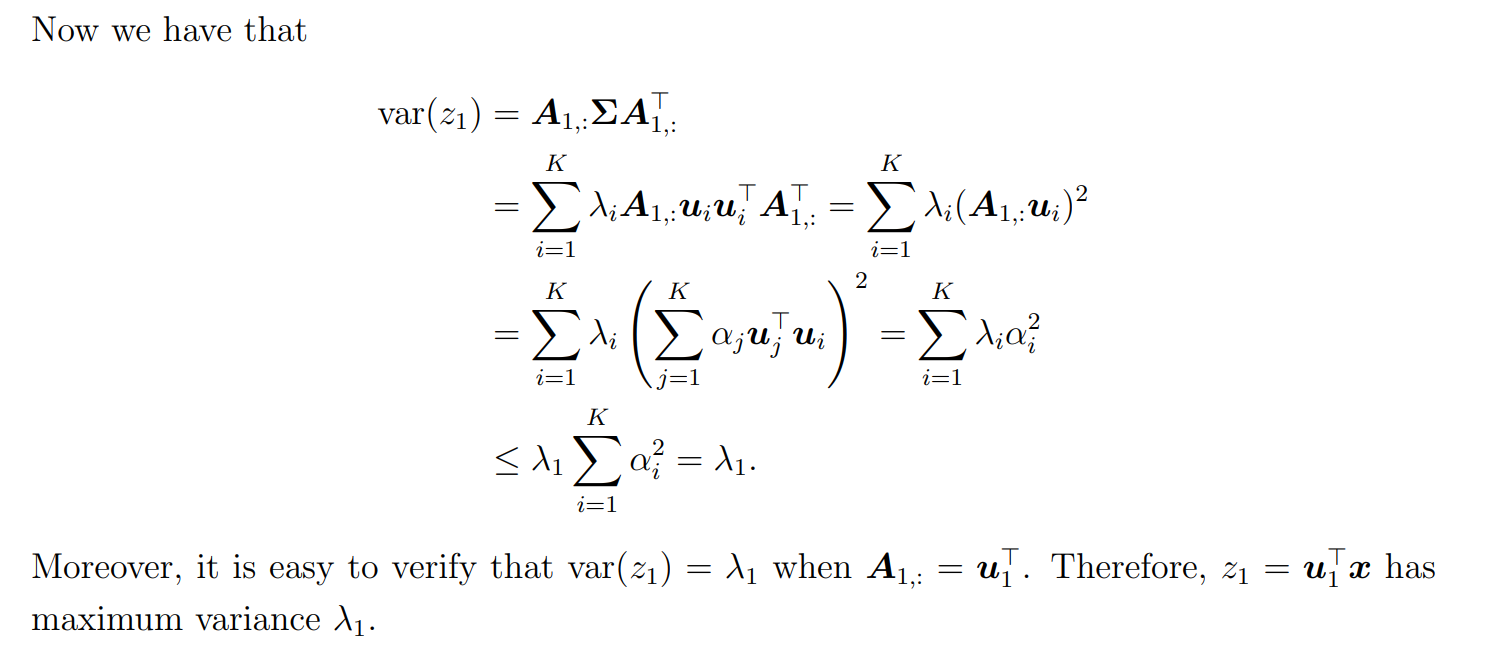
image.png

image.png

奇异值分解 (Singular Value Decomposition, SVD)

  • 目标： SVD是一种纯粹的矩阵分解技术，它的目标是将任何一个矩阵 A 分解为三个特定矩阵的乘积： ​
    • U：左奇异向量矩阵，是一个正交矩阵。它的列向量构成了原始数据行空间的一组标准正交基。
    • Σ：奇异值对角矩阵。对角线上的元素称为奇异值（Singular Values），非负且从大到小排列。奇异值衡量了对应奇异向量方向上的“重要性”或“能量”。
    • V：右奇异向量矩阵，也是一个正交矩阵。它的列向量构成了原始数据列空间的一组标准正交基。是它的转置。

PCA是一种思想/方法，SVD是一种数学计算工具。

image.png