为什么要使用批次?从计算效率谈起
基本定义回顾:
- Epoch(回合): 模型完整地看过一次所有训练资料。
- Batch(批次): 在一个Epoch内,我们将所有资料分成若干份,每一份就是一个Batch。模型每看完一个Batch,就进行一次参数更新。
- Iteration(迭代): 每更新一次参数,就算一次迭代。因此,迭代次数 = Batch的数量。
Small Batch 与 Large Batch
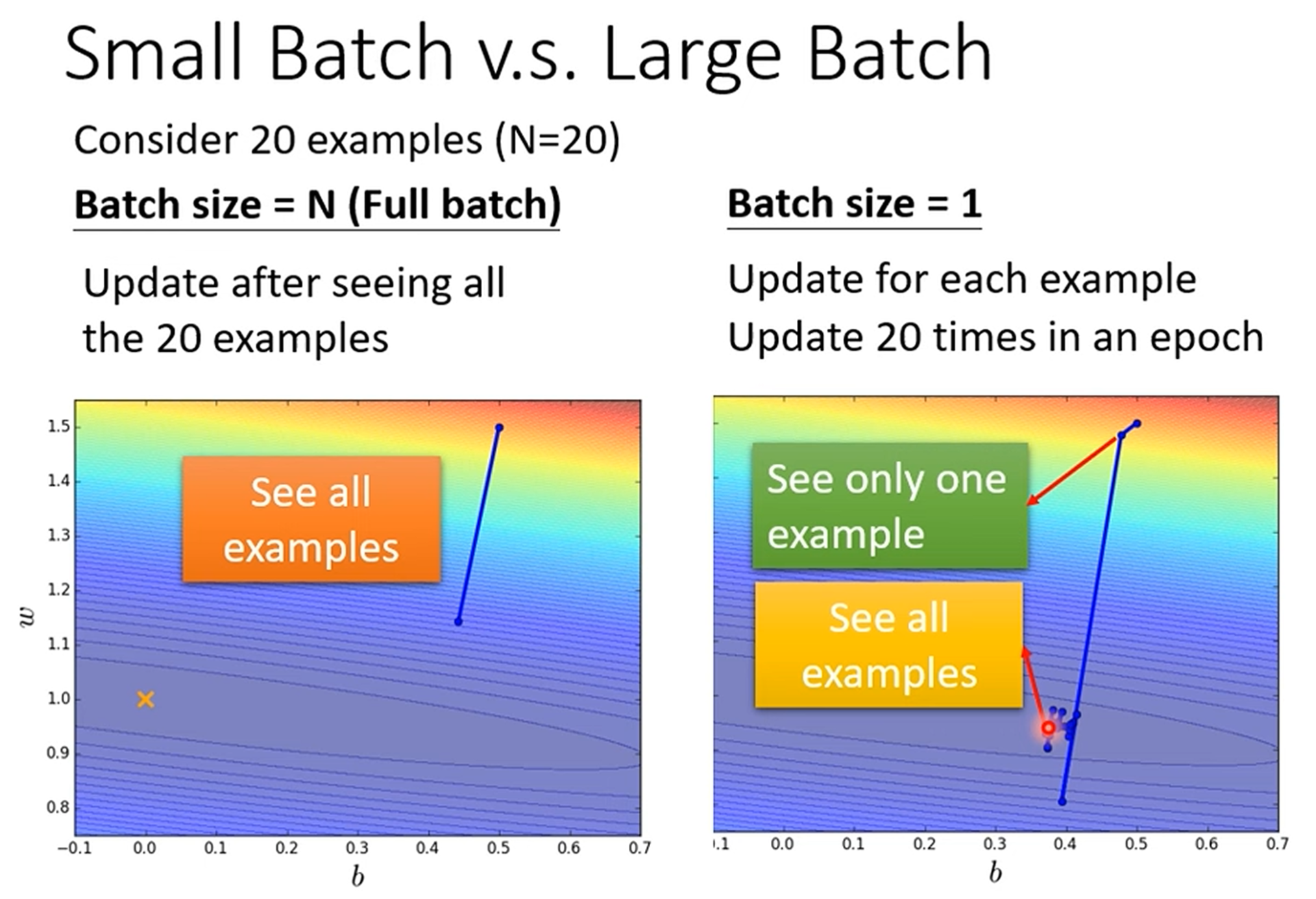
分析large Batch用时:
大的batch有平行计算加持,其实并不比小batch慢
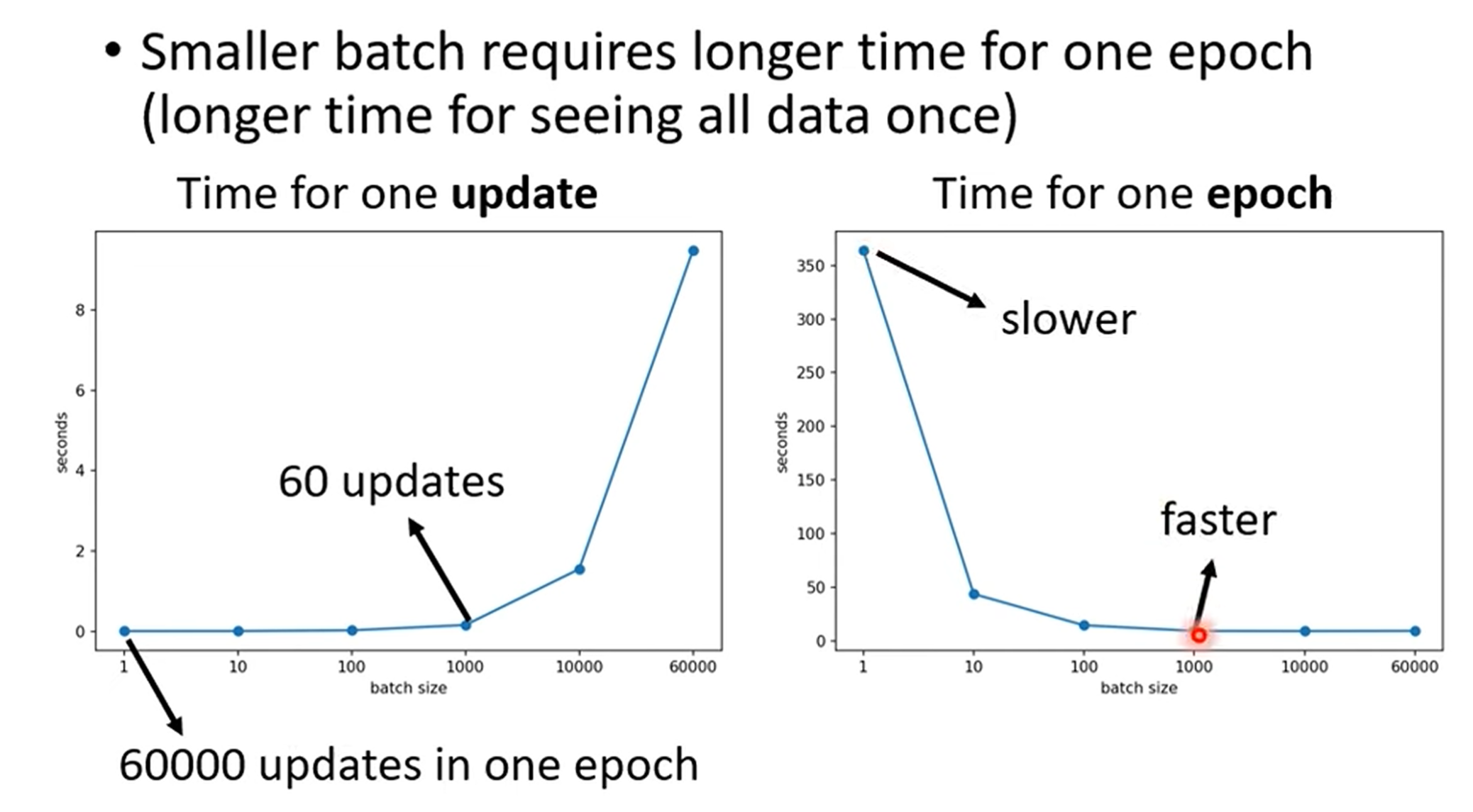
分析Small Batch 用时:
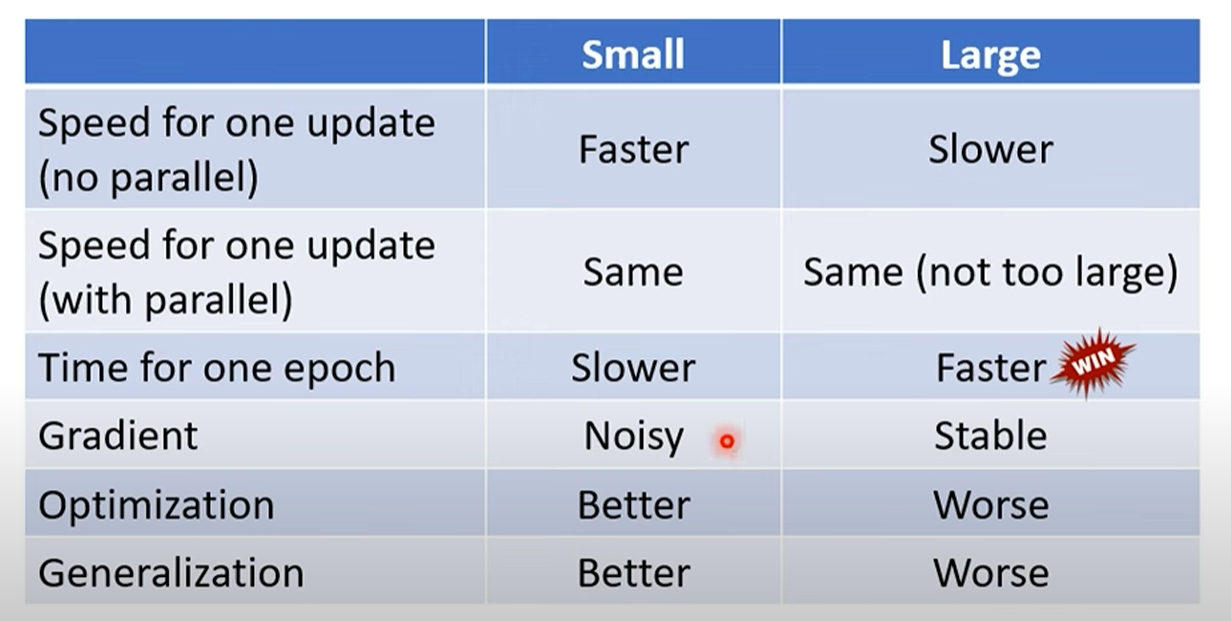
算整个epoch的时候,其实小batch,不一定算快
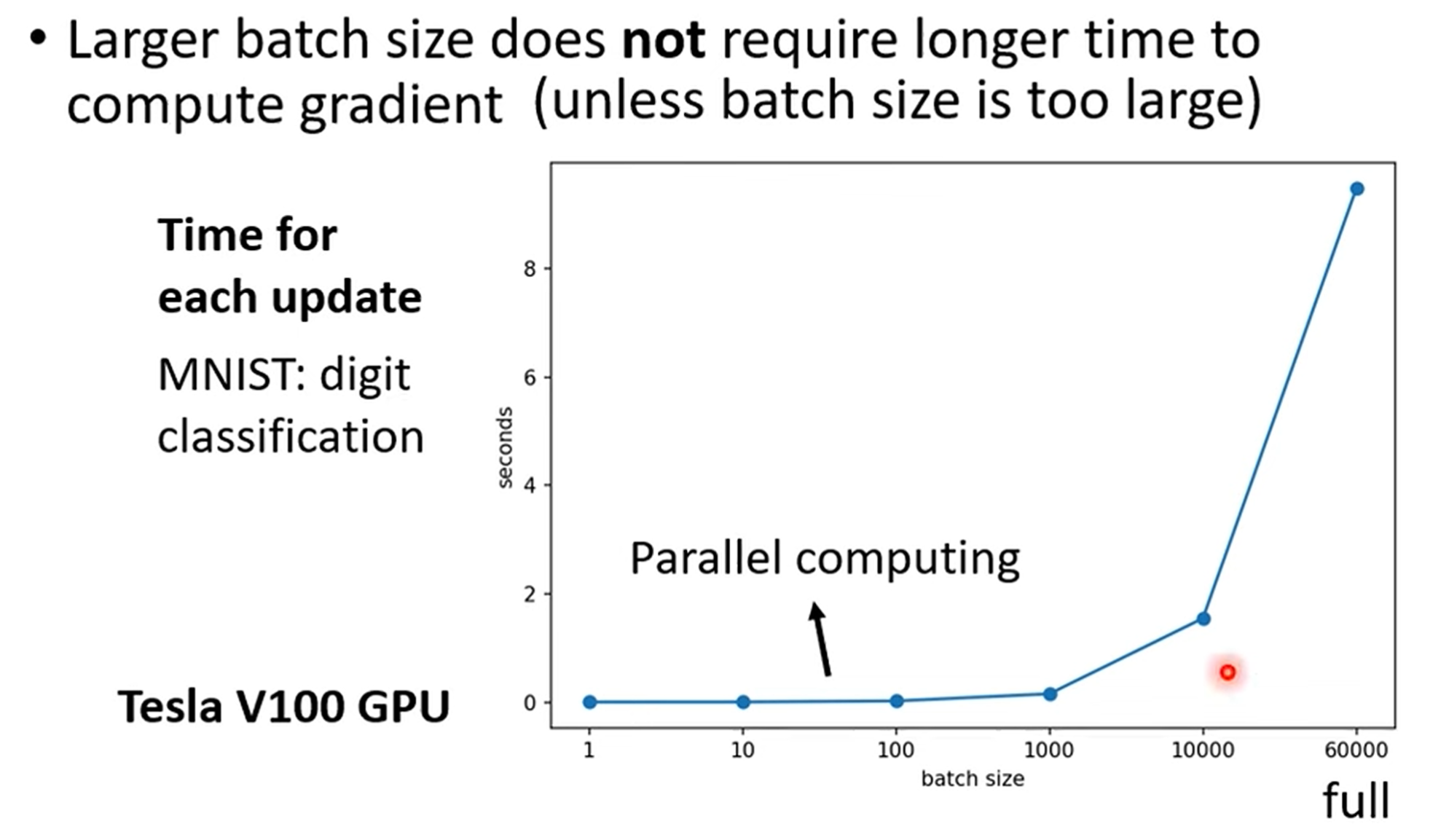
重点讲解:GPU并行计算带来的反直觉效率
- 直觉误区: Batch Size越大,包含的样本越多,计算梯度所需时间应该越长。
- 关键洞察:这个直觉是错误的!展示的实验数据显示,在GPU上,将Batch Size从1增加到1000,完成一次梯度计算和参数更新所需的时间几乎没有变化。
- 深度原因:GPU是为大规模并行计算而生的。无论是处理1个样本还是1000个样本的矩阵运算,GPU都能“同时”处理。因此,只要Batch Size没有大到超出GPU的并行处理能力上限,单次迭代的时间成本是相对固定的。
- 时间成本结论:
- 完成一个Epoch的总时间 = 单次迭代时间 × 迭代次数。
- 由于大Batch Size的单次迭代时间与小Batch Size相近,但它的迭代次数要少得多(例如,60000笔资料,Batch Size=1000需要60次迭代,而Batch Size=1需要60000次迭代),因此使用大Batch Size跑完一个Epoch通常更快。
Small Batch的优点:
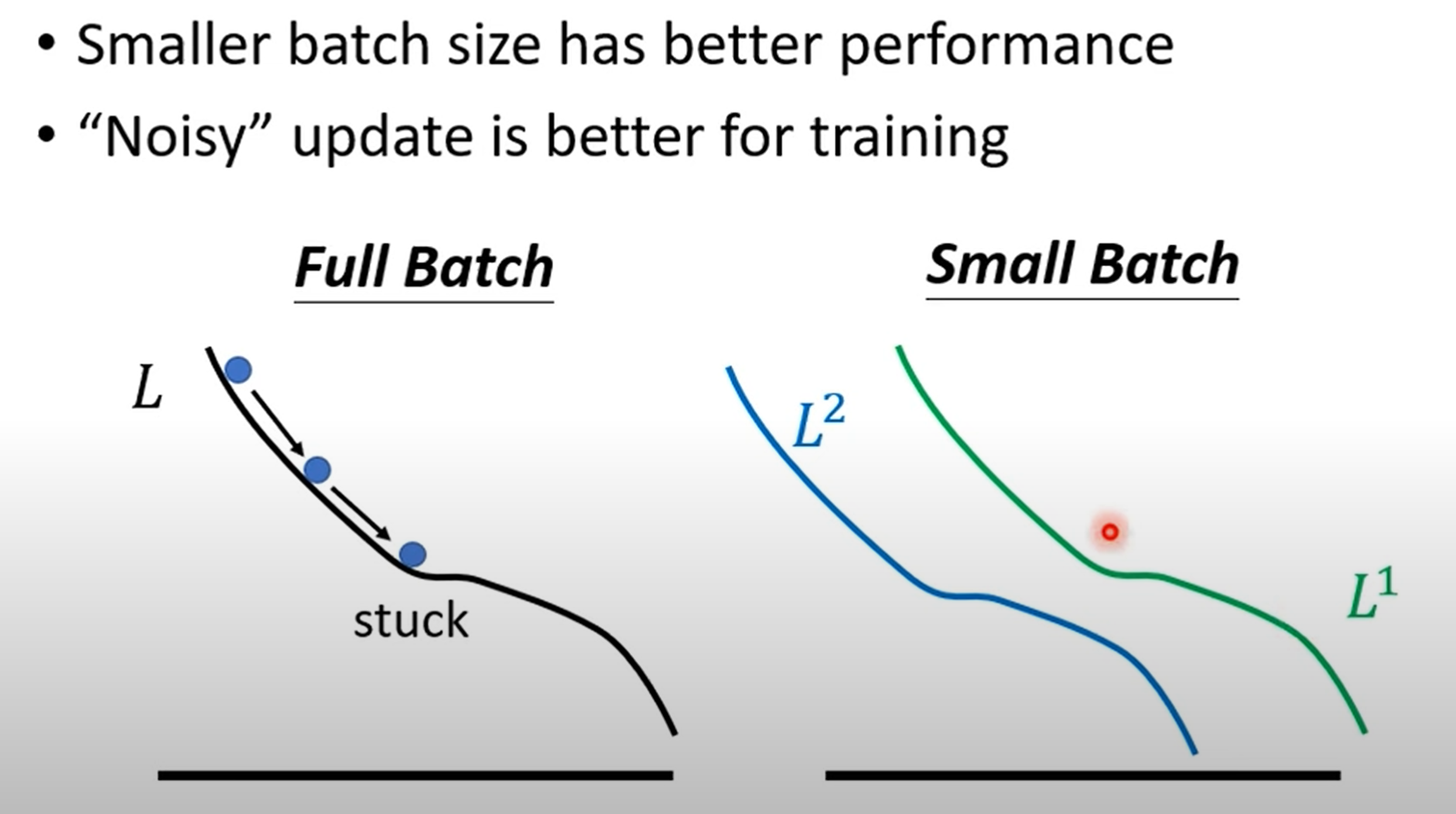
小批次的惊人优势:从“噪声”中获益
如果大批次更快,我们为什么不总是用它呢?下一部分给出了颠覆性的答案:训练效果。
重点讲解(一):“带噪声的梯度”有助于优化
- 实验现象:实验结果清晰表明,Batch Size越小,最终在验证集(Validation Set)上得到的准确率越高。这意味着小批次在“优化”这个任务上做得更好。
- 理论解释:
- 大批次(Full Batch)的困境:当使用全部数据计算梯度时,梯度方向是“精准”且“稳定”的。如果模型不幸陷入一个局部最小值点或鞍点(梯度为零),参数更新就会完全停止,因为它认为自己已经到达了最优位置。
- 小批次的“智慧”:小批次每次只看一部分数据,因此它计算出的梯度方向是带有“随机性”或者说“噪声”的。当一个批次的数据让模型陷入局部最小时,下一个批次的数据会计算出一个全新的、几乎肯定不同的梯度方向,从而轻松地将模型“拽出”这个陷阱。
- 生动比喻:可以想象成下山。大批次就像一个非常谨慎的登山者,只沿着最陡峭的路走,一旦走进一个山谷(局部最小),就出不来了。而小批次则像一个不断探索的登山者,虽然每一步看起来有些随机,但这种探索性让他能绕过小山谷,最终找到通往山脚(全局最小)的更好路径。
不同的局部最小值的好坏:
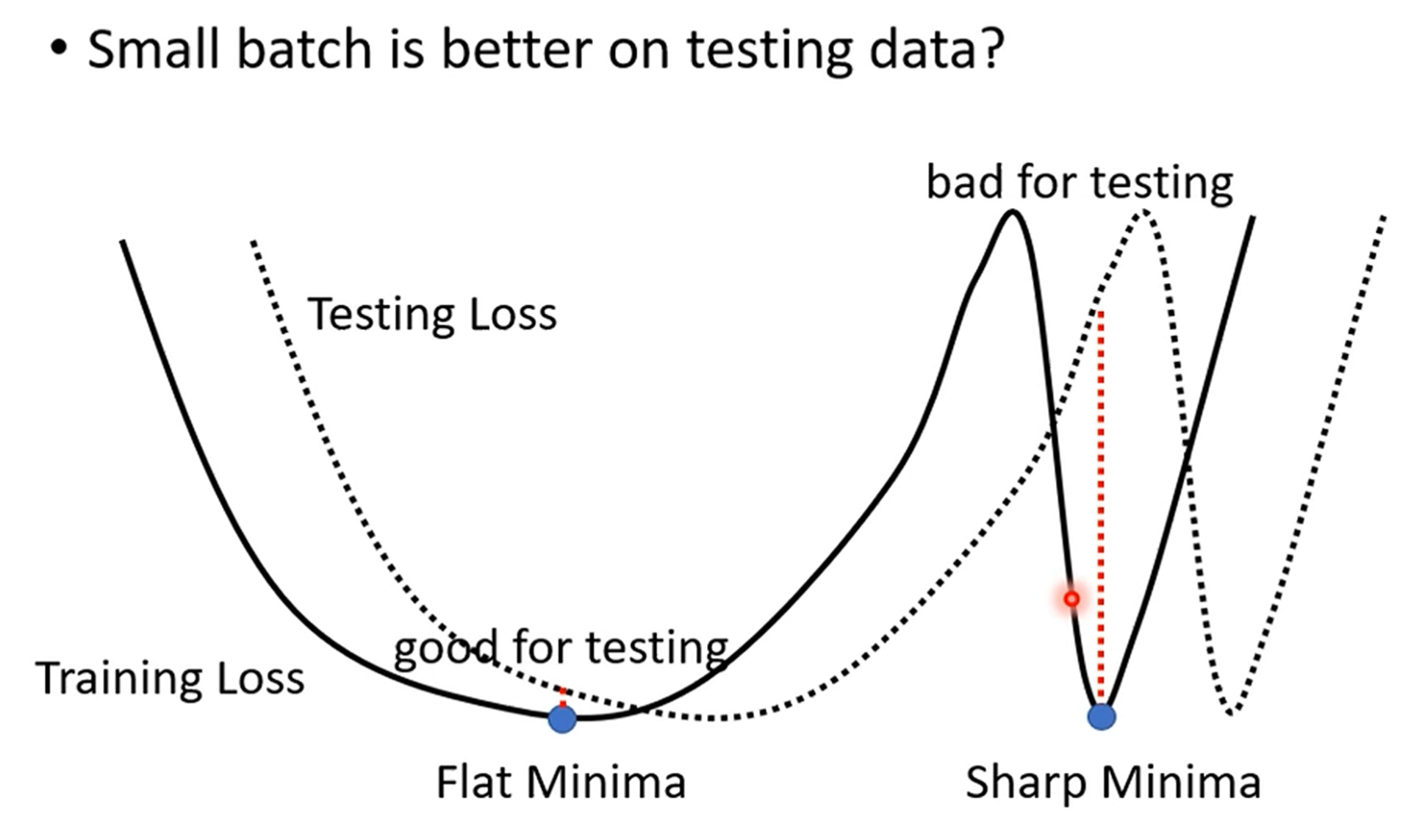
重点讲解(二):小批次能找到“更好”的最小值,提升泛化能力
核心问题:为什么小批次训练的模型在**测试集(Test Set)**上表现更好?这涉及到模型的泛化能力。
“宽阔”与“狭窄”的最小值 (Wide vs. Sharp Minima):这是视频中最重要、最细致的讲解部分。
- Sharp Minima (坏的最小值):想象一个非常尖锐、狭窄的峡谷。你的模型在训练集上找到了这个谷底,Loss非常低。但是,测试集的数据分布与训练集总有微小的差异。这个差异就可能导致在测试时,你的位置偏离了谷底一点点,而由于峡谷非常陡峭,你的Loss会急剧上升,性能大幅下降。大批次由于其稳定的下降方向,很容易找到并陷入这种“看似最优”的尖锐峡谷。
- Wide Minima (好的最小值):想象一个宽阔、平坦的盆地。你的模型在这里找到了一个Loss很低的区域。当面对测试集时,即使数据分布的差异让你的位置有了少许偏移,但因为你身处一个平坦的盆地中,Loss的变化非常小,模型性能依然稳健。这种最小值具有更好的泛化能力。
为什么小批次能找到Wide Minima? 小批次的“噪声”是关键。因为每一步的更新方向都在抖动,模型很难在一个尖锐的峡谷底部稳定下来。为了在各种噪声的干扰下还能保持较低的Loss,模型“被迫”去寻找一个宽广的、对扰动不敏感的区域。因此,噪声在这里扮演了“正则化”的角色,帮助模型找到了更鲁棒(robust)的解
最终结果:
借助物理角度引入Momentum
传统梯度下降法:
梯度下降加Momentum
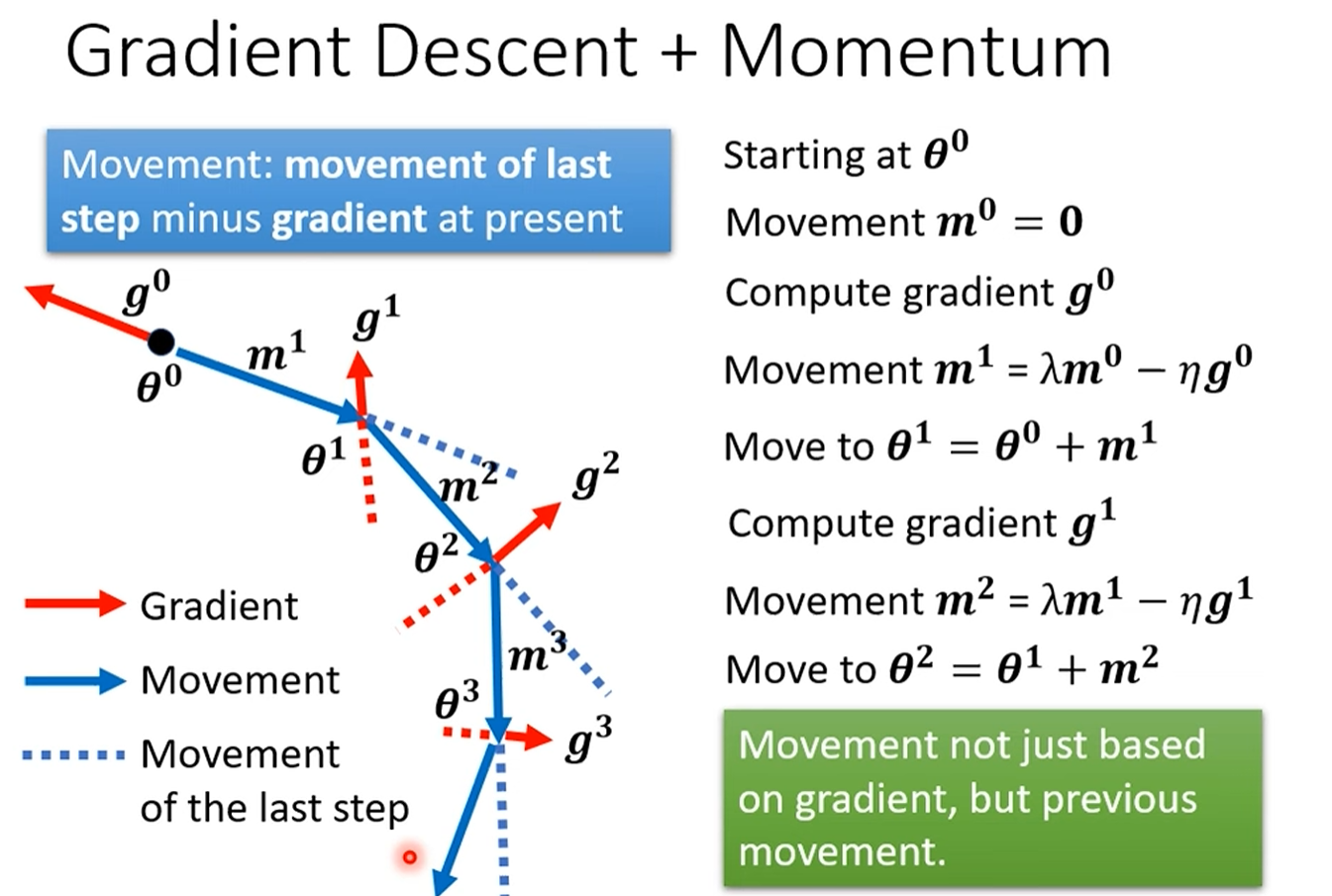
动量(Momentum)—— 赋予梯度下降“惯性”
如果说Batch Size是从数据层面进行优化,那么Momentum则是从更新算法本身进行改进。
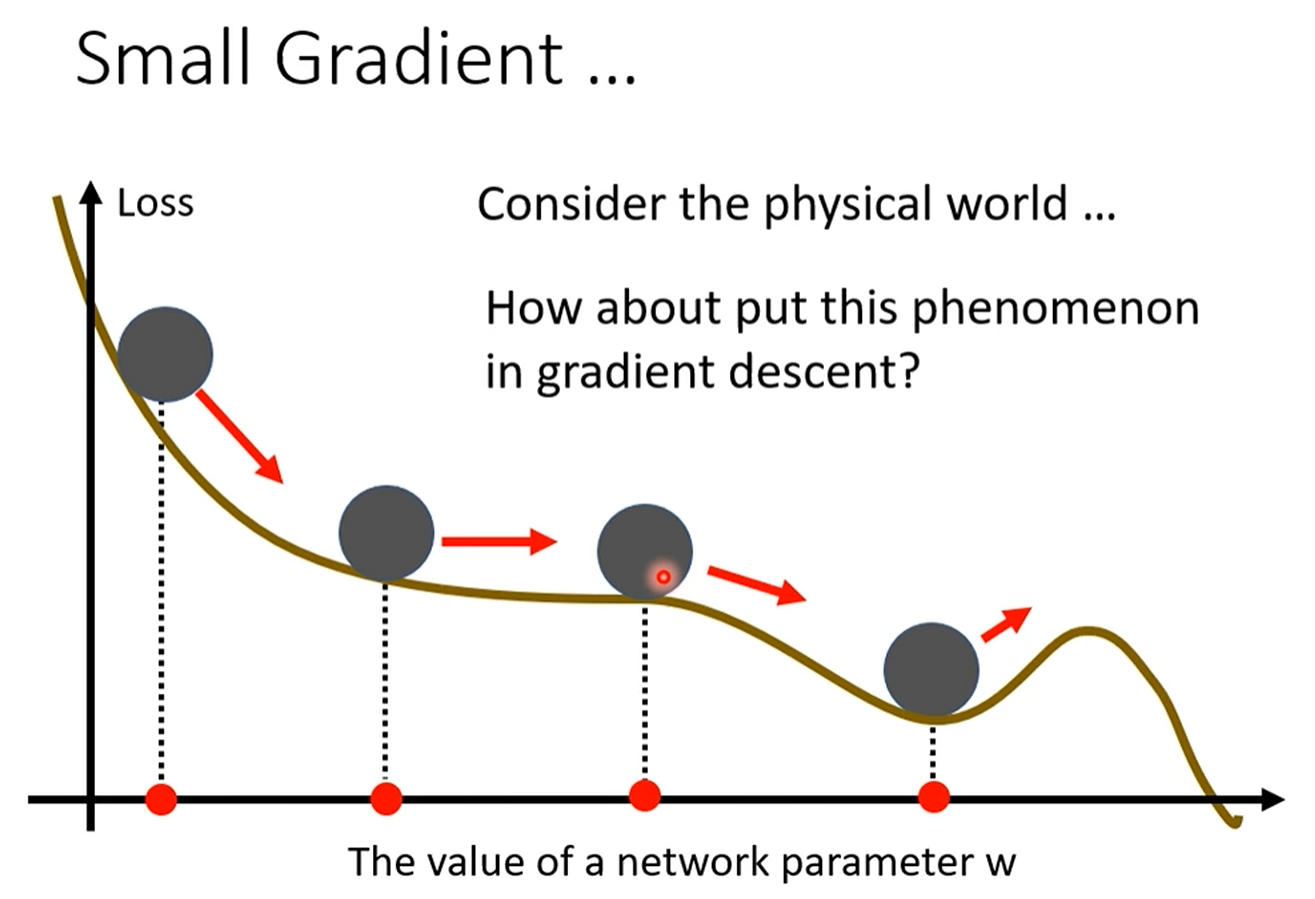
核心思想:物理世界中的惯性
标准梯度下降的缺陷:它是一个“健忘的”算法,每一步只考虑当前所在位置的梯度,不关心历史。这导致它在平坦区域(梯度小)会移动缓慢,在局部最小值点(梯度为零)会直接停下。
Momentum的类比:引入物理学中“动量”的概念。一个从高处滚下的小球,积累了速度(动量)。当它遇到一个小的凹坑(局部最小)或者一段平路时,它不会立即停下,而是会因为惯性继续向前冲,甚至能冲出凹坑,翻过小山坡。
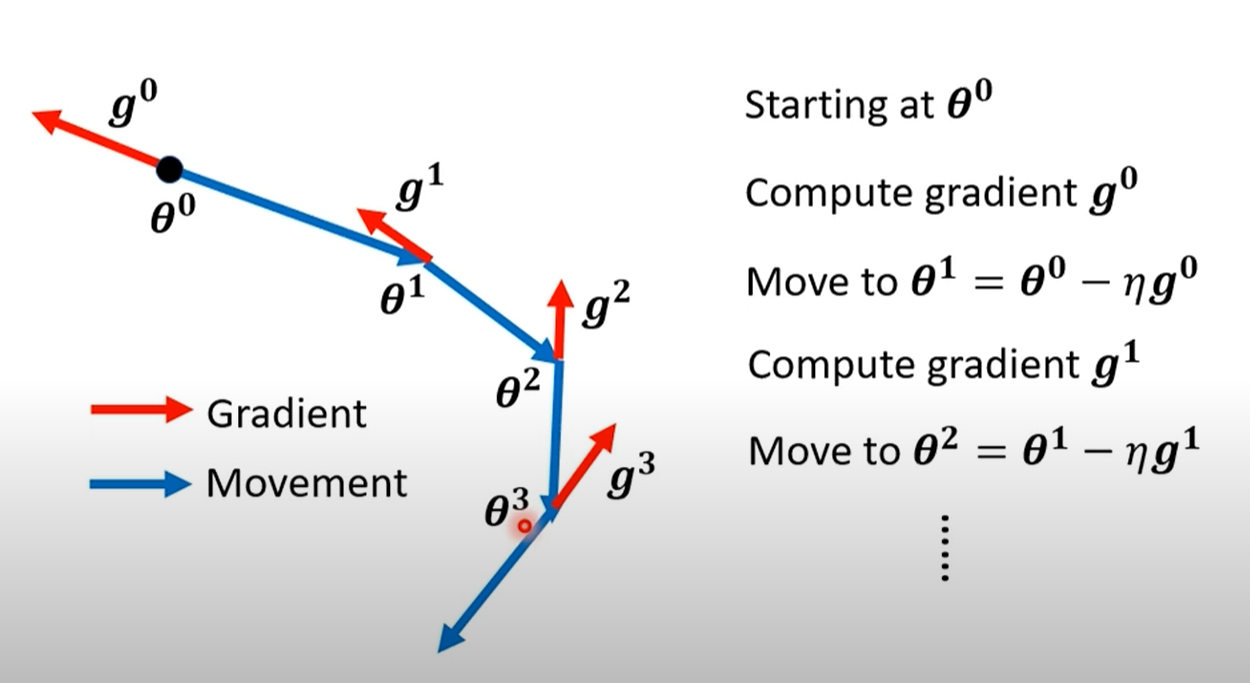
重点讲解:Momentum的运作机制
数学公式拆解:
- 每一次的移动
由两部分构成: :这是当前批次计算出的梯度,代表了当前最快的下降方向。 :这是上一步的移动量,代表了历史积累的“惯性”或“动量”。 (lambda):这是一个介于0和1之间的超参数,通常设为0.9。它代表了“动量”的衰减率,或者说“摩擦力”。 λ越大,历史动量的影响就越大,惯性越强。
- 每一次的移动
工作流程:参数更新的方向不再仅仅是当前梯度的反方向,而是上一步移动方向和当前梯度反方向的加权和。这意味着,模型会“记住”它之前的移动方向。
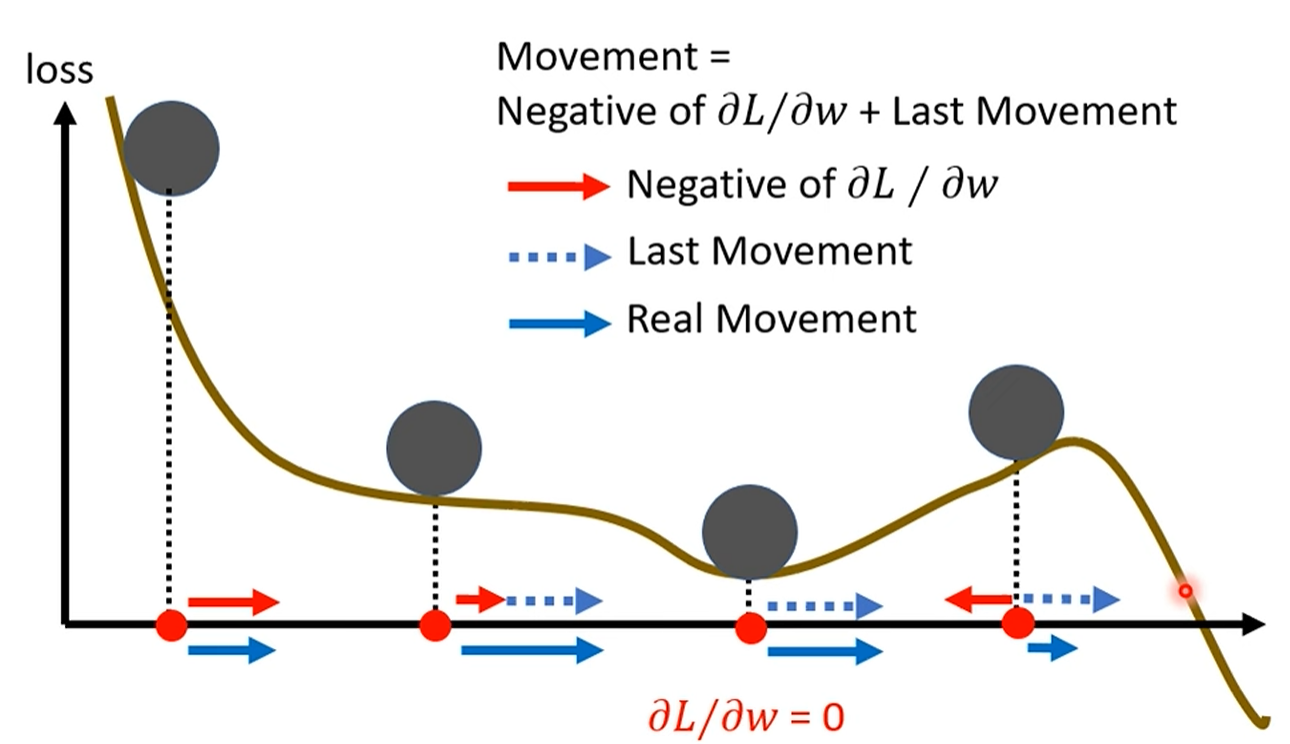
- 带来的巨大优势:
1. 加速学习:在梯度方向基本不变的区域,动量的累积效应会使得参数更新的步长越来越大,从而加速收敛。
2. 穿越鞍点/平原:在鞍点或平坦区域,g_t可能非常小甚至为零。没有Momentum的算法会在此处“熄火”。但Momentum因为有m_{t-1}的存在,依然可以保持移动,穿越这些棘手的地形。
3. 摆脱局部最小:就像小球的惯性一样,累积的动量有足够的力量帮助模型“冲出”一些比较浅的局部最小值陷阱。
reference:
图片来自:【機器學習2021】類神經網路訓練不起來怎麼辦 (二): 批次 (batch) 與動量 (momentum)
