测度论:
σ-field
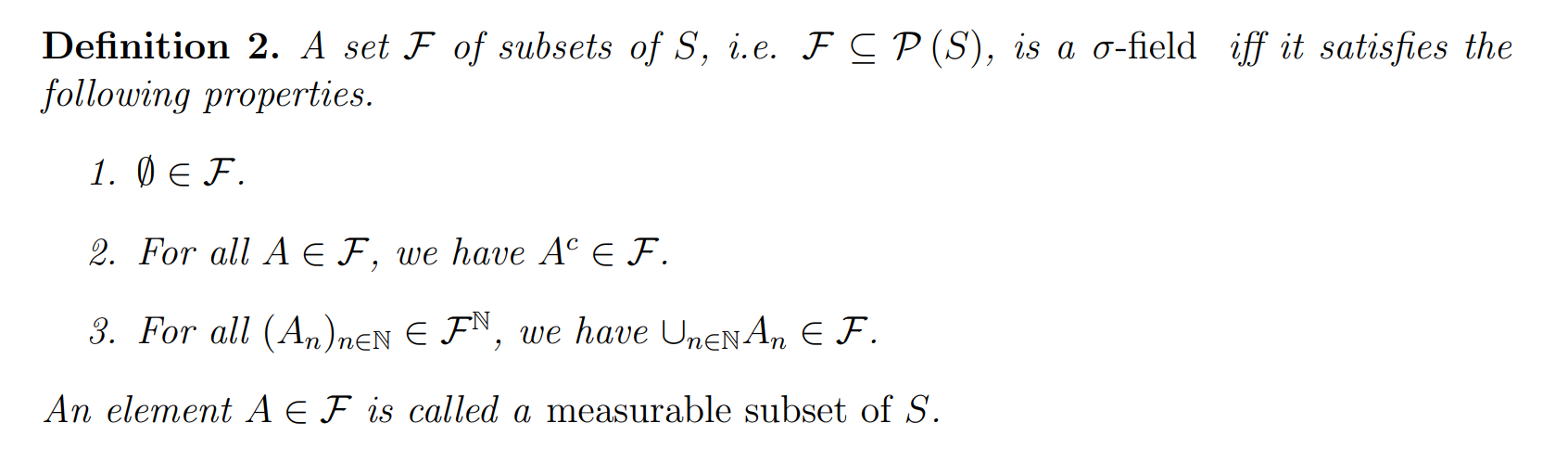
field和σ-field:
区别在于性质三:field要求有限unions属于F
σ-field要求可数unions属于F
Borel σ-field

注意:
术语:
Measurable spaace
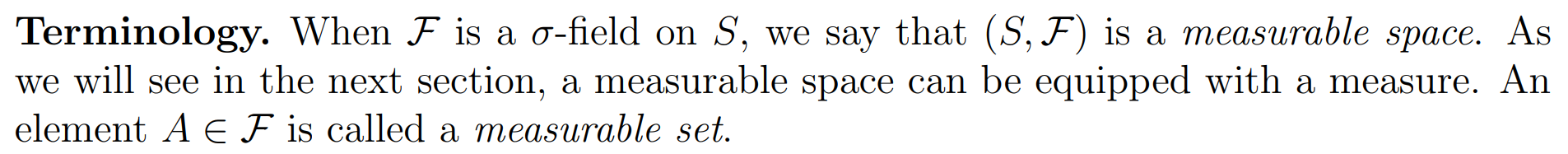
Measure

Measured space
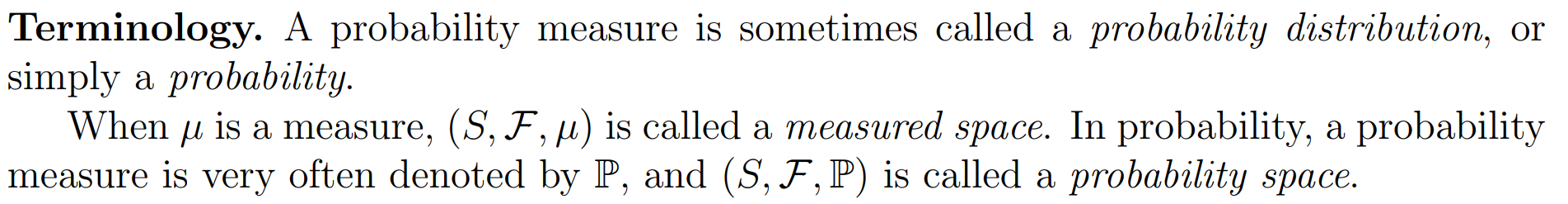
关系网

finite measure and probability measure

probabilities(常用于证明)

注意:
- 全集S带进去,概率等于1.
Measure种类:
Counting measure
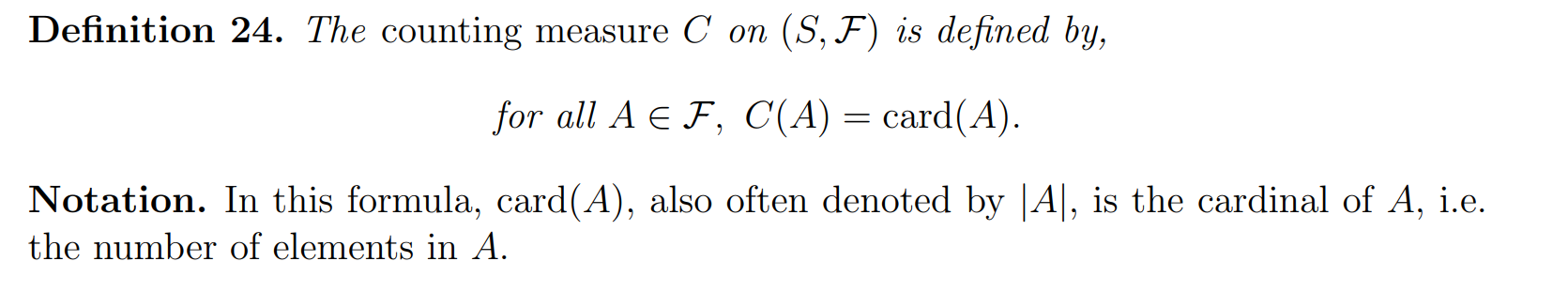

格式:
cdf :
Independent
Independent of random variable
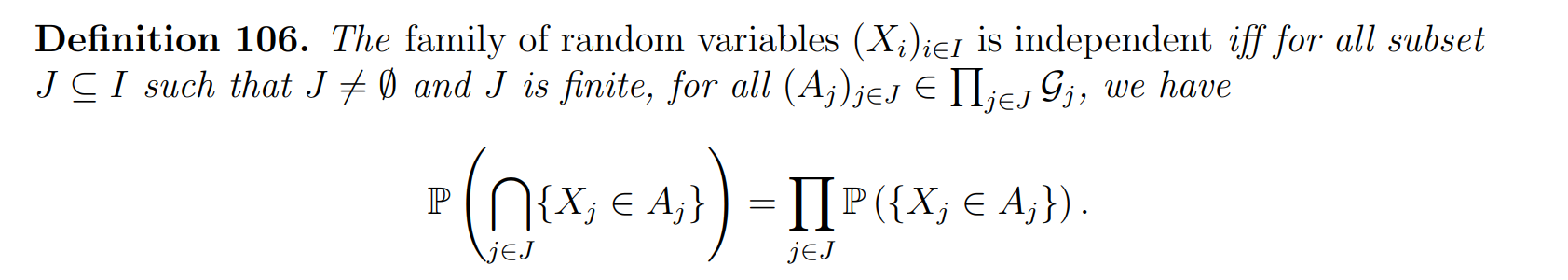
定义两个随机变量:
:第一次掷硬币的结果,设为 1 表示正面,0 表示反面; :第二次掷硬币的结果,定义同上。
我们设概率空间
每个事件概率为
设
我们来看这两个随机变量是否独立。
根据定义,对所有集合
我们需要验证:
De Morgan’s Laws
Joint distribution


例题分析:

考试题目分析

题目a:
由于y收到x的影响,先对y积分方便,y积分的范围是(0,x),x积分的范围是(0,+∞)
题目b:
marginal Y :x积分范围(y,+∞),
marginal X :没争议,y积分范围是(0,x)

Conditional Expectation
对事件:

对随机变量:

推导过程:

性质:

例题分析:

条件期望和期望的关系:
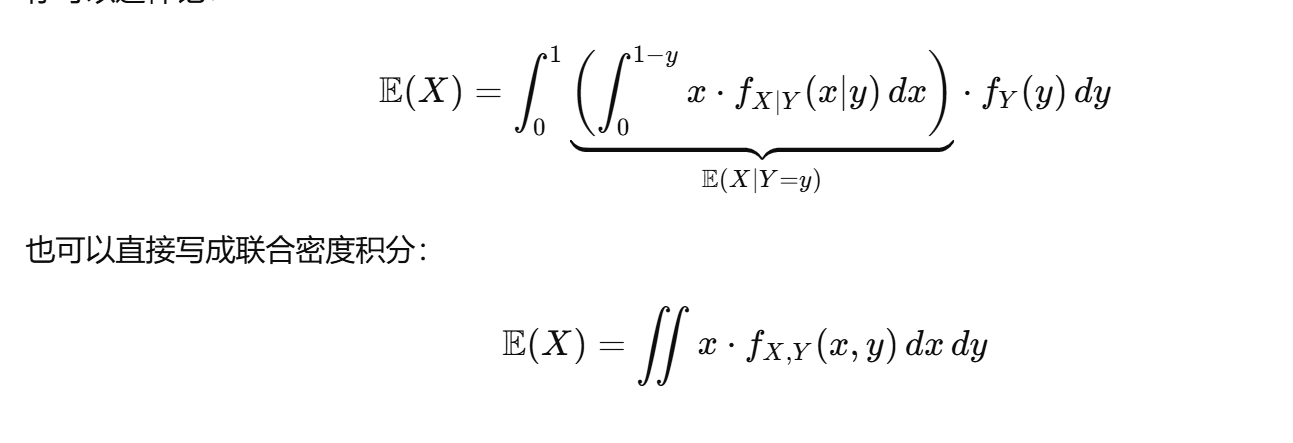
Variance,Covariance
方差的性质:
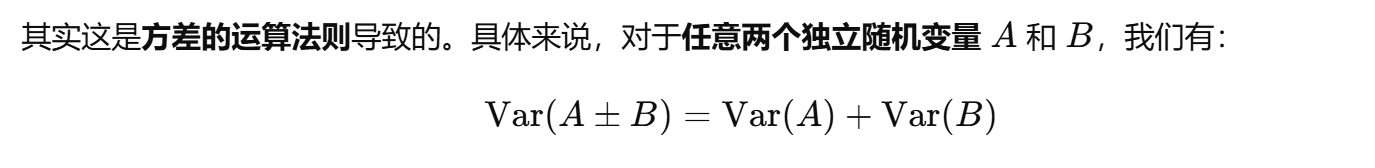

协方差:
定义:
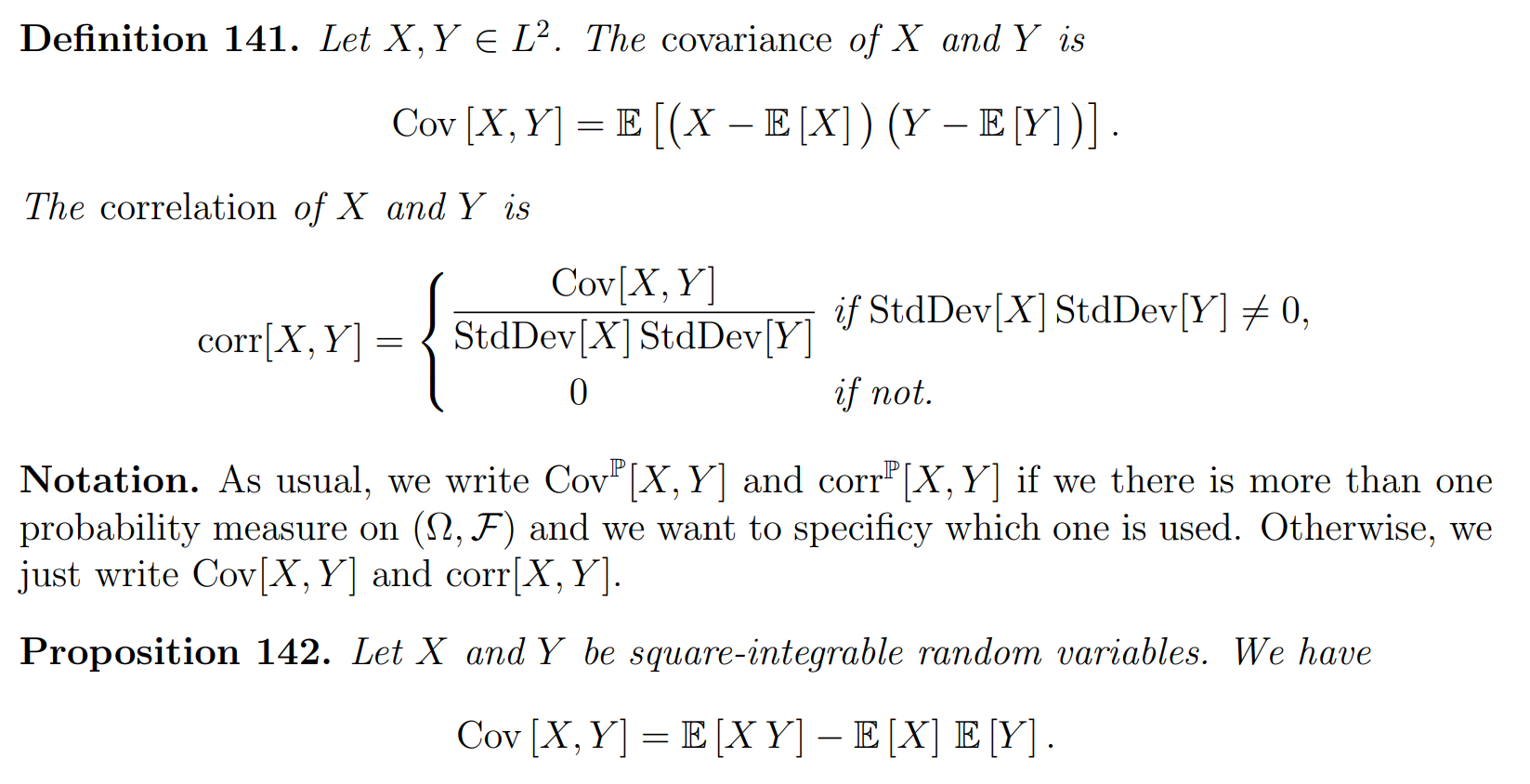
性质:

Chebyshev inequality
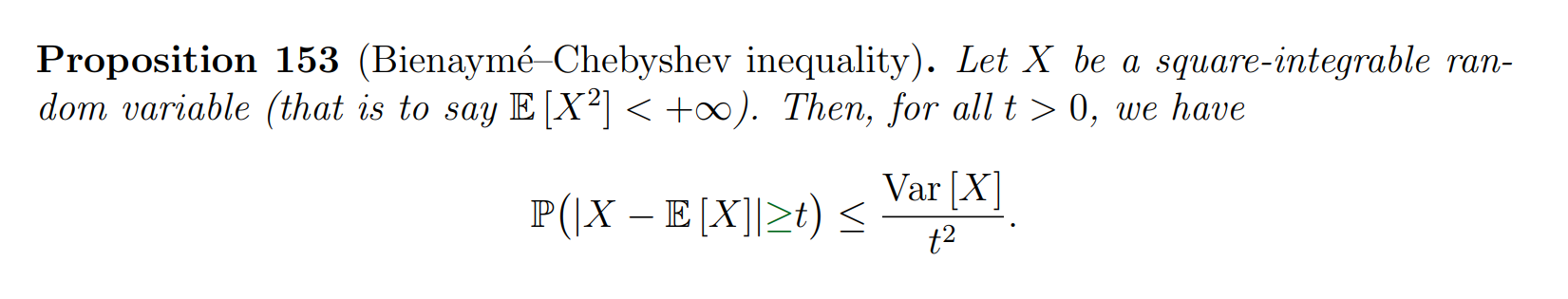
Moment-generating functions
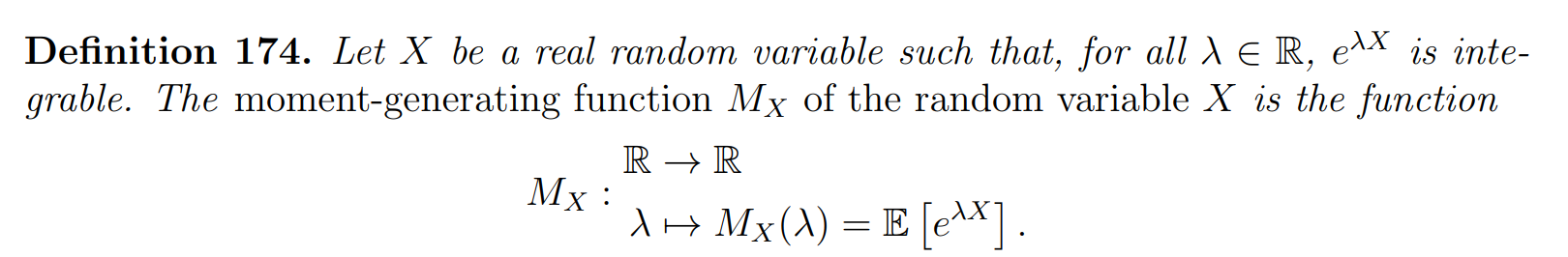

概率分布
极值分布问题(min(X1,X2),max(X1,X2))

伯努利分布(Bernoulli distribution)
pmf
期望:
方差:
指数函数
cdf
尾部概率
正态分布:
pdf:
$$
f_X(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}}, \quad x \in \mathbb{R}
$$
cdf:
泊松分布:
pdf:
cdf:
$$
P(X \leq k) = \sum_{i=0}^k \frac{\lambda^i e^{-\lambda}}{i!}
$$
期望
方差
几何分布
pdf:
期望:
方差:
中心极限定理:

以Poisson分布为例:
$$
$$
补充标准化的细节:

参数估计
MME:
Def of Moment
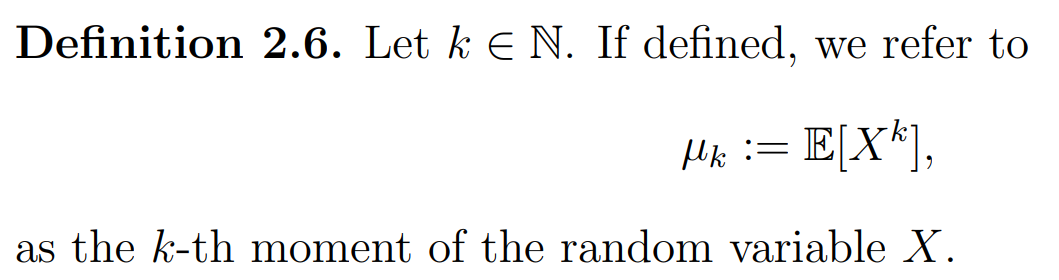
Def of MME

例题:
MLE:

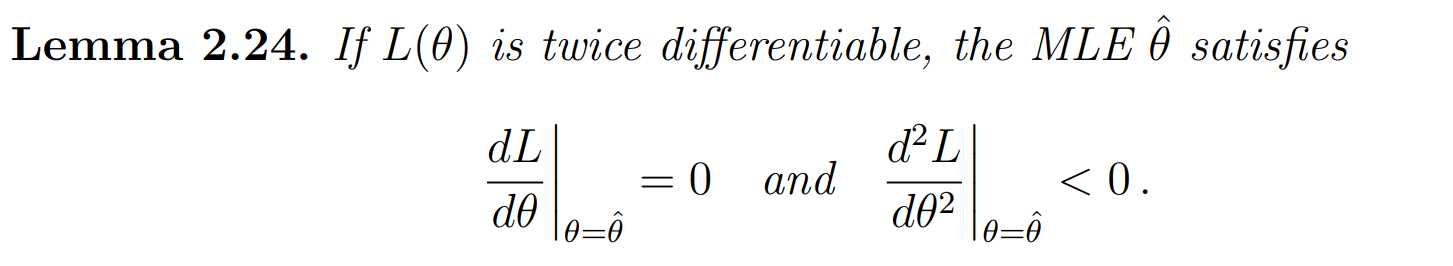
已知观测值计算似然值

CRLB:

n足够大的时候,用于构造置信区间

最后这个区间是
置信区间
求解

基于MLE的置信区间(作业):


统计假设检验:
统计假设检验的组成
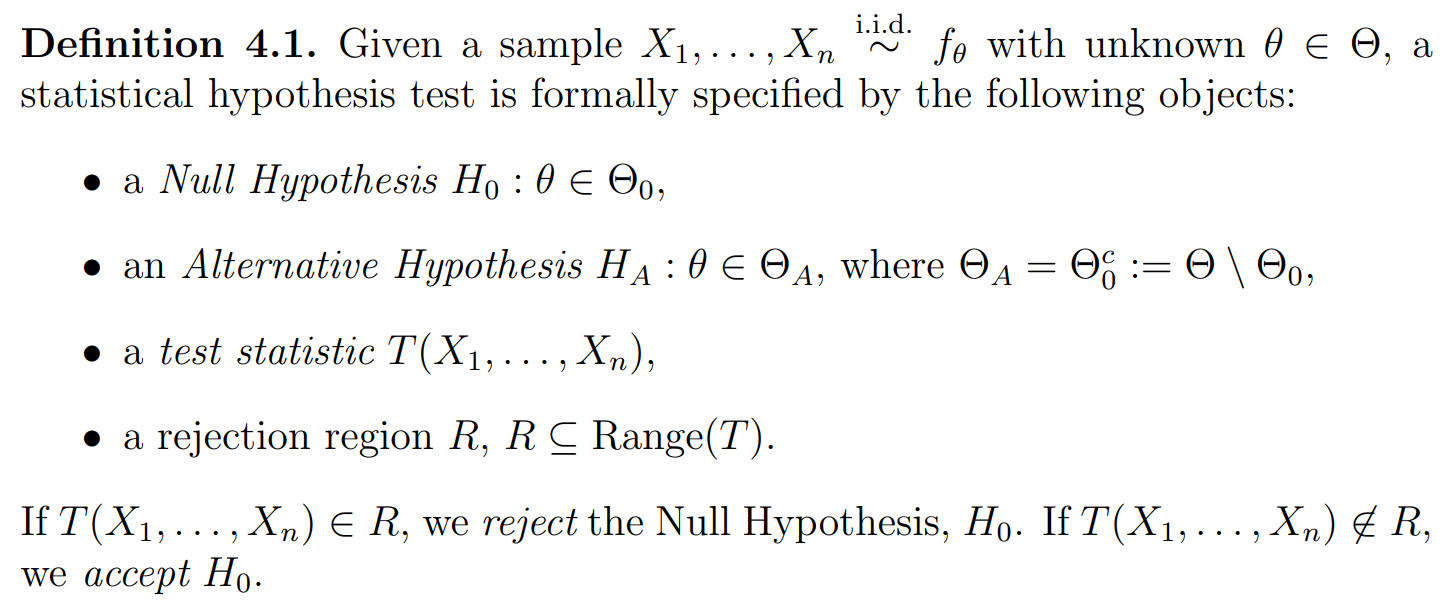
Type I and II error

常考点:test statistic 有 z-test ,t-test,chi-square-test.

Size of test

Power of test

最强MPtest:



离散情况是小于等于

例题解析:
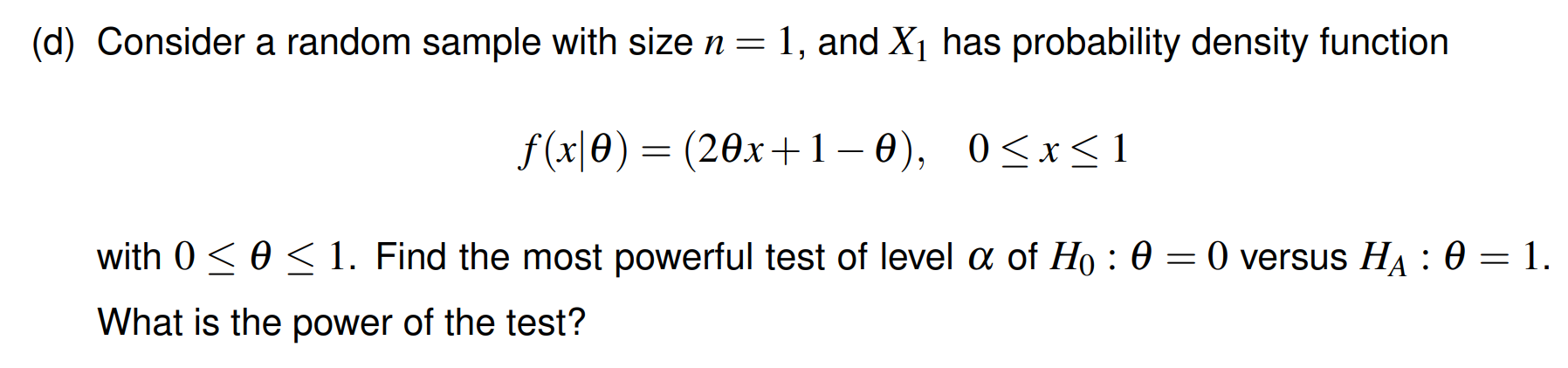

两个独立正态分布样本

Obtain an estimate of the common variance.
已知相同的方差下:样本方差的关系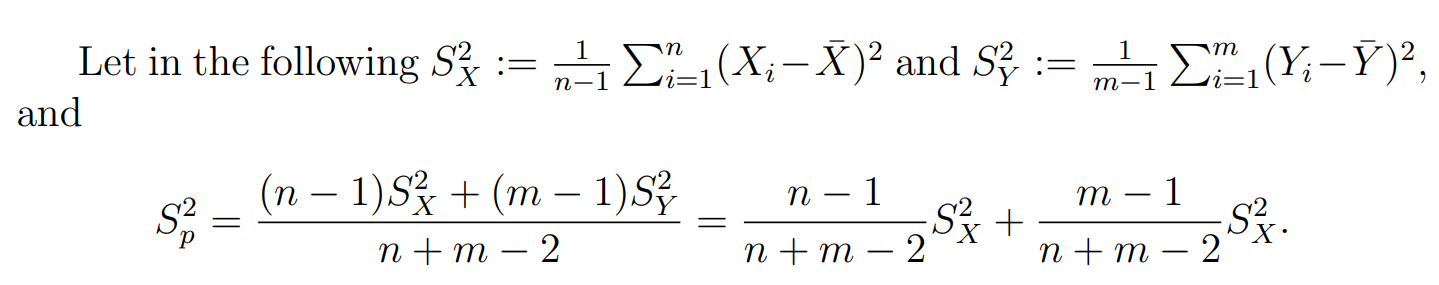
标准化

求解
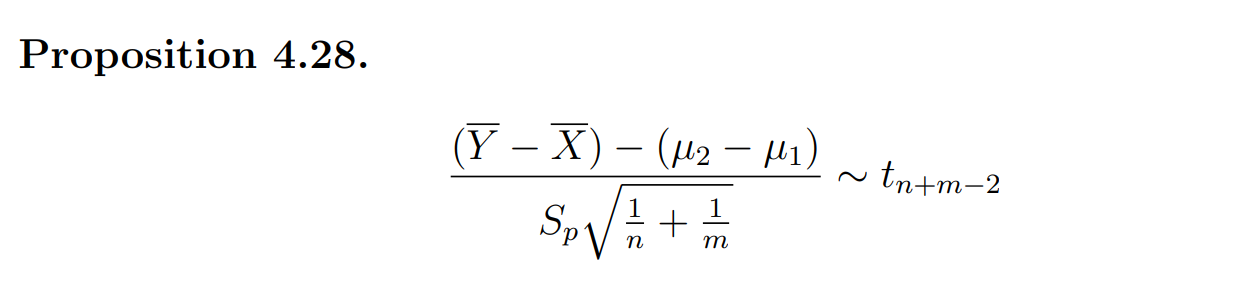
求解方差:
一个正态分布:
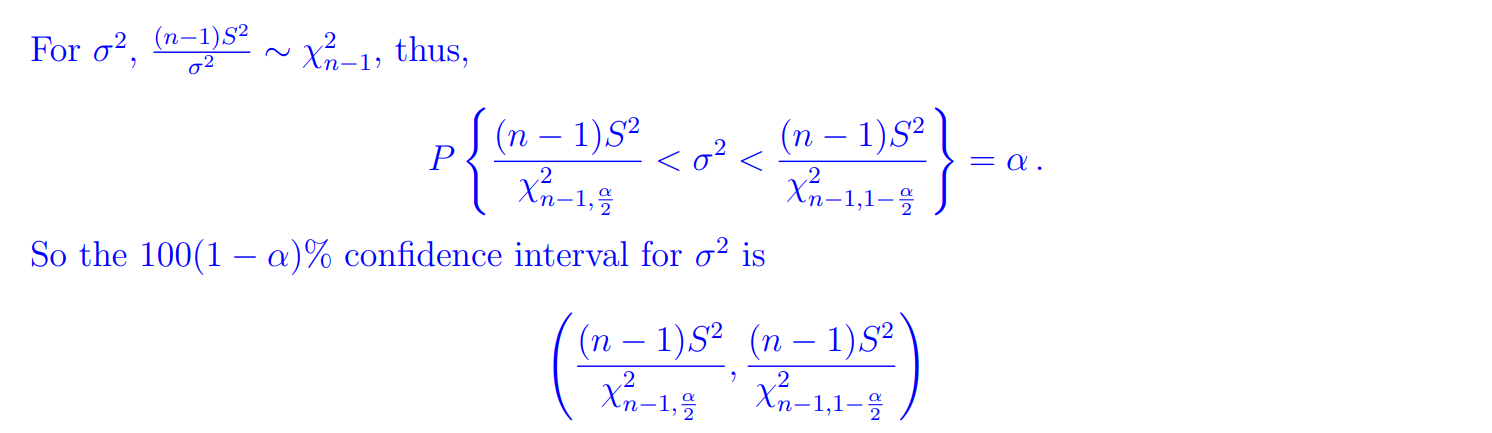
两个正态分布
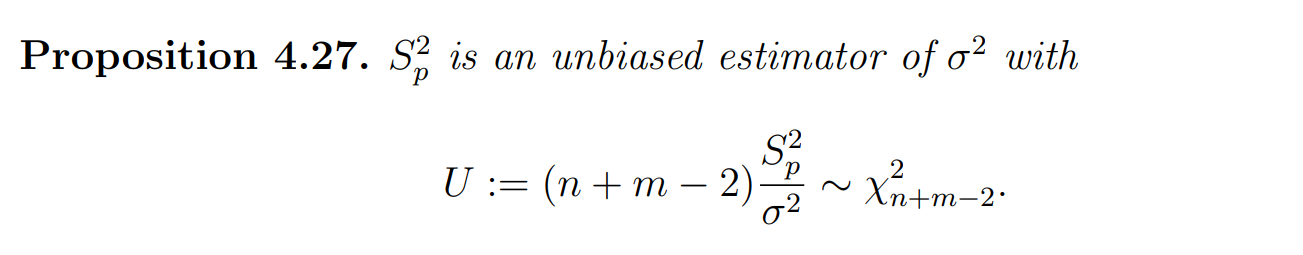
例题:


解析一下:
b和c的区别:
b:是求出来其中之一的方差(无论是X的还是Y都用同一个方差)
c:是用估计的方差,近似真实的方差
线性回归:
线性回归的定义:

最小二乘法角度:

定义残差:

求解β
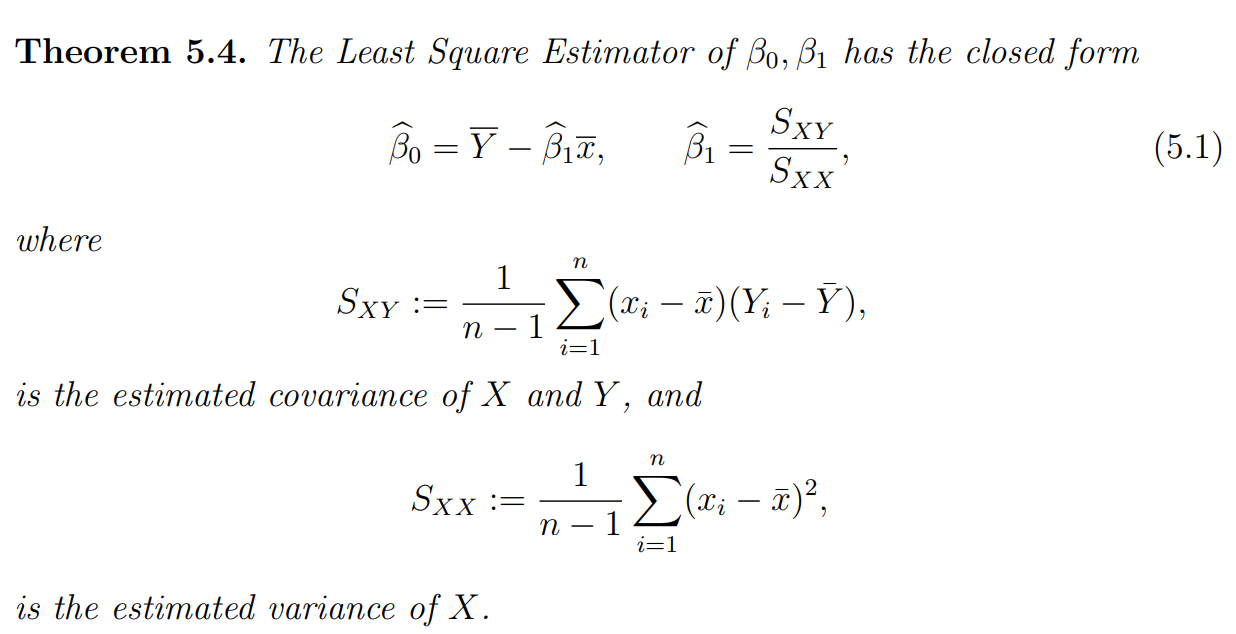
推导过程:

线性回归性质:

Convergence of random variables
Almost-sure convergence
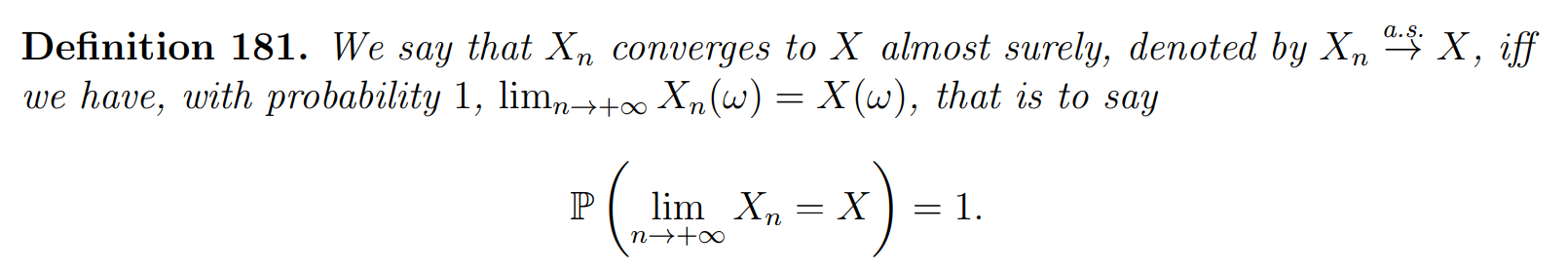
Convergence in probability
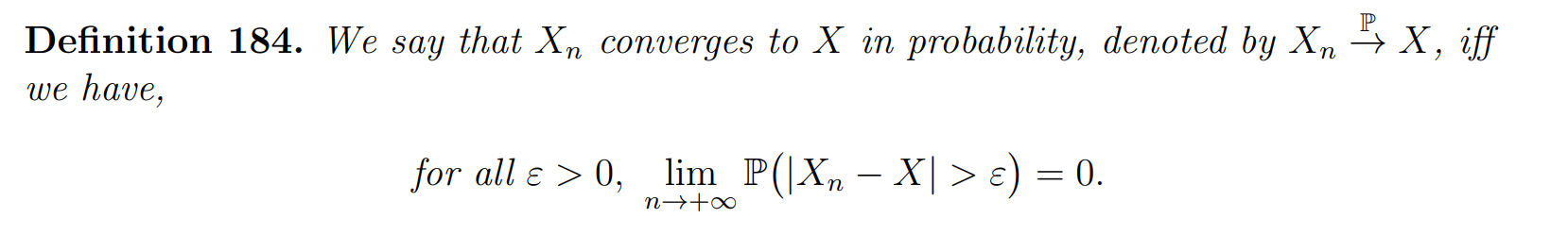
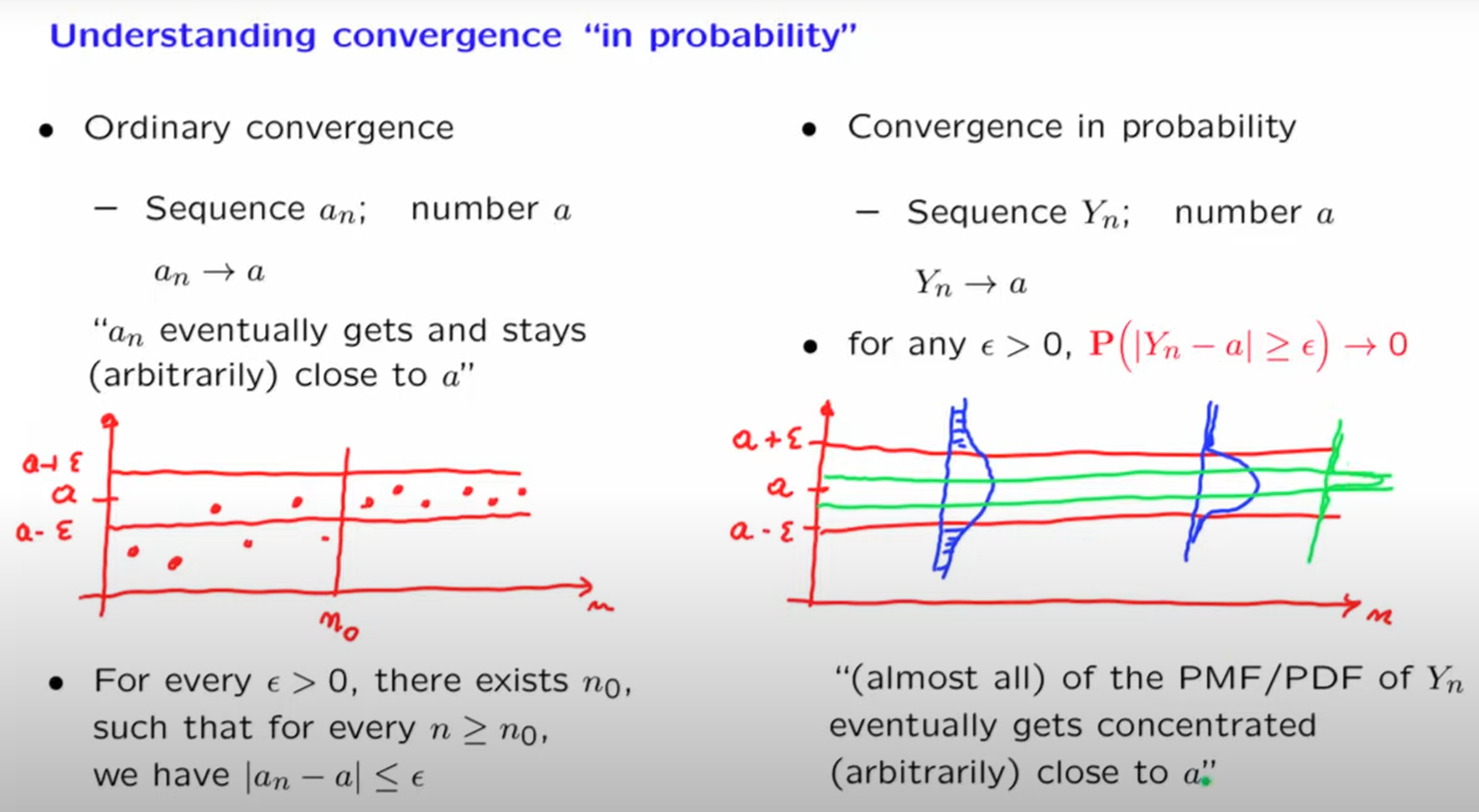
Convergence of distributions
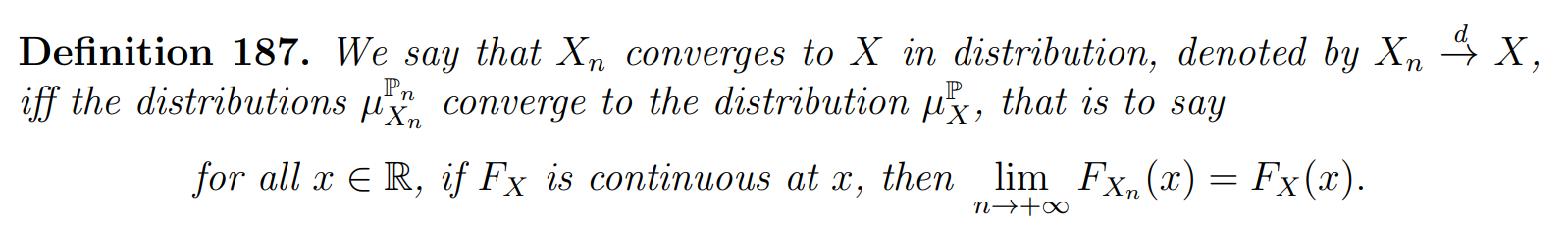
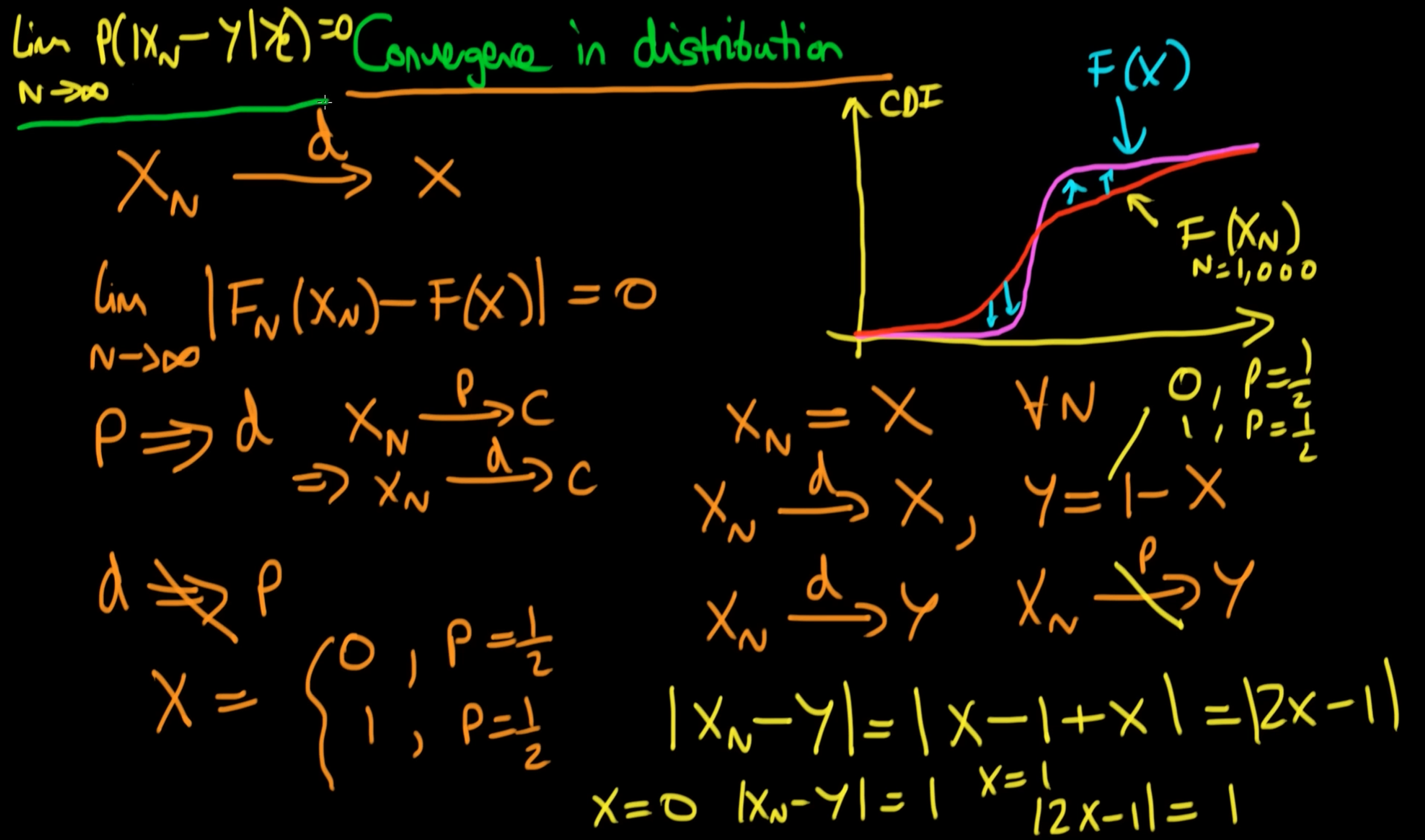
反例:
分布收敛,概率不收敛


- 现在,我们选择一个
,例如 (任何小于1的正数都可以)。 - 我们来计算概率
:
- 这个概率对于所有的
都恒等于 ,它不会收敛到 。 - 因此,
不依概率收敛于 。
分布收敛于常数,概率也收敛



拟合优度类检验(Goodness-of-Fit Tests)


fitted parameters 就是分布中的未知参数的数量,这些参数在检验过程中是用样本数据估计出来的,因此会消耗自由度。

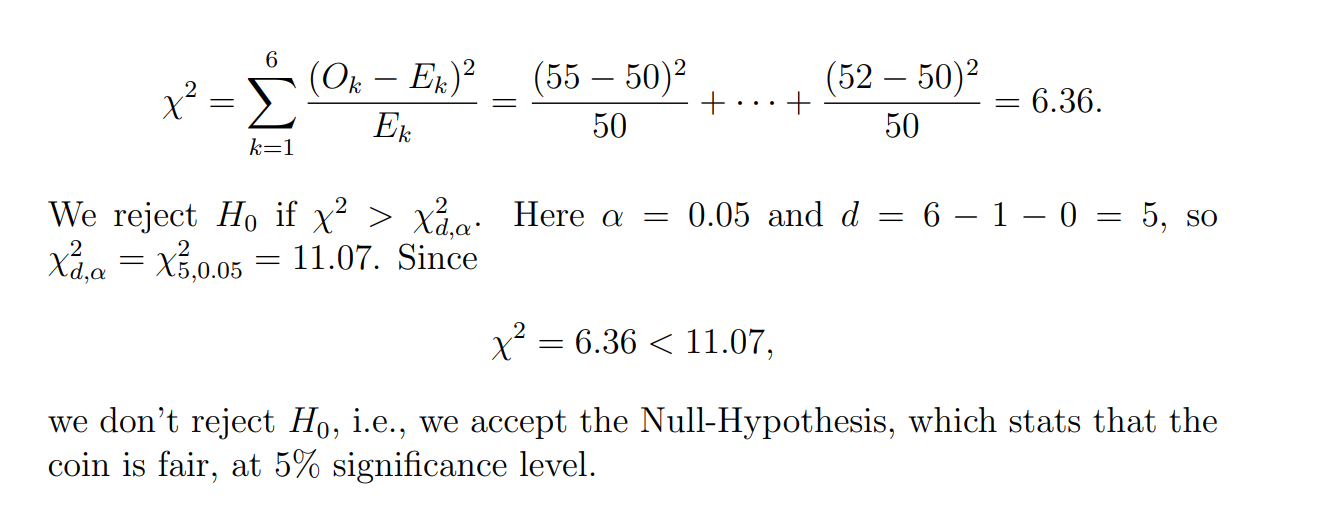
Test 总结:


