我们了解了机器学习的基本三部曲。然而,简单的线性模型在面对复杂现实世界问题时,往往会显得力不从心。我们将打破线性模型的局限,正式迈向更强大、更灵活的“深度学习”世界。
线性模型的“偏见” (Model Bias)
线性模型的根本问题:模型偏见(Model Bias)。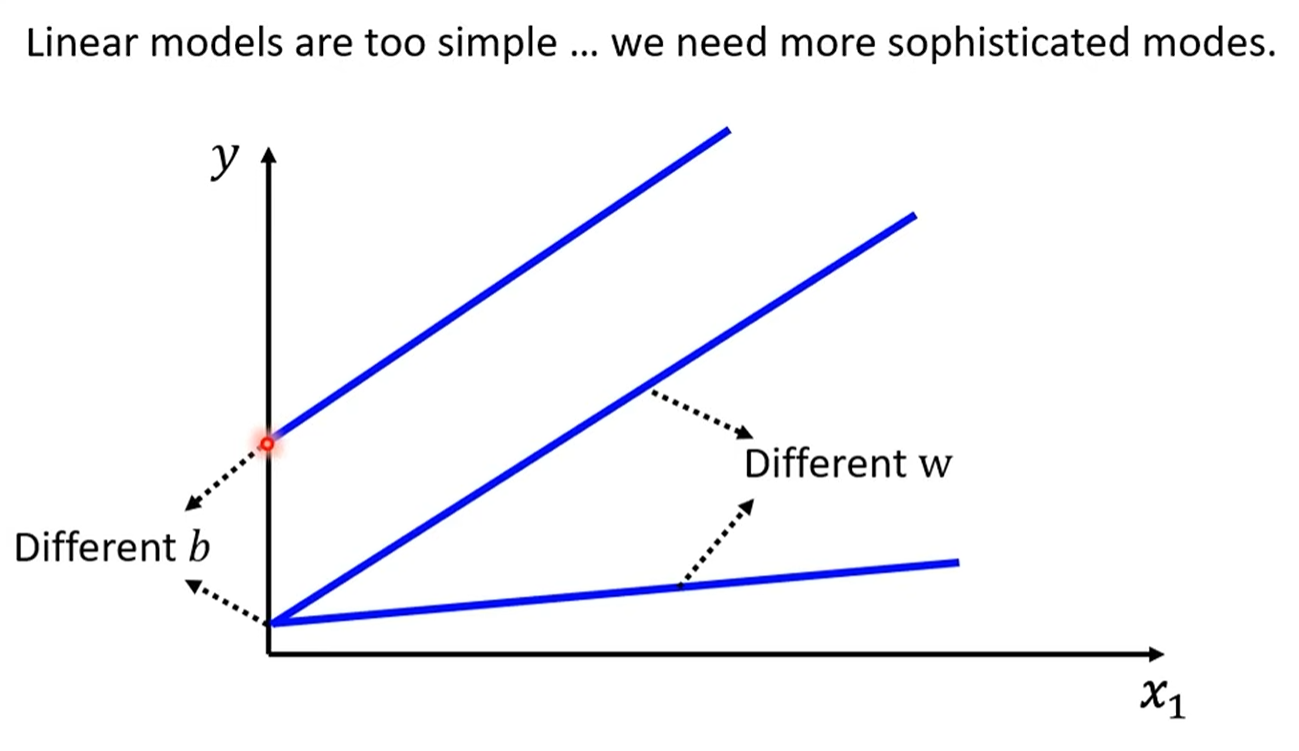
核心概念:线性模型本身的结构过于简单,它假设输入和输出之间是纯粹的线性关系。这导致它无法捕捉现实世界中普遍存在的非线性规律。例如,YouTube的观看人数可能并不会一直线性增长,而是会呈现复杂的周期性波动。
重要区分:这里的“Model Bias”指的是模型本身的限制,与我们之前提到的作为模型参数的“bias”(偏置项
b)是两个不同的概念。解决方案:要解决这个问题,我们必须构建一个更复杂、更有弹性的函数模型。
如何构建更复杂的函数?
用一个非常直观的方式,为我们揭示了构建复杂函数的秘诀: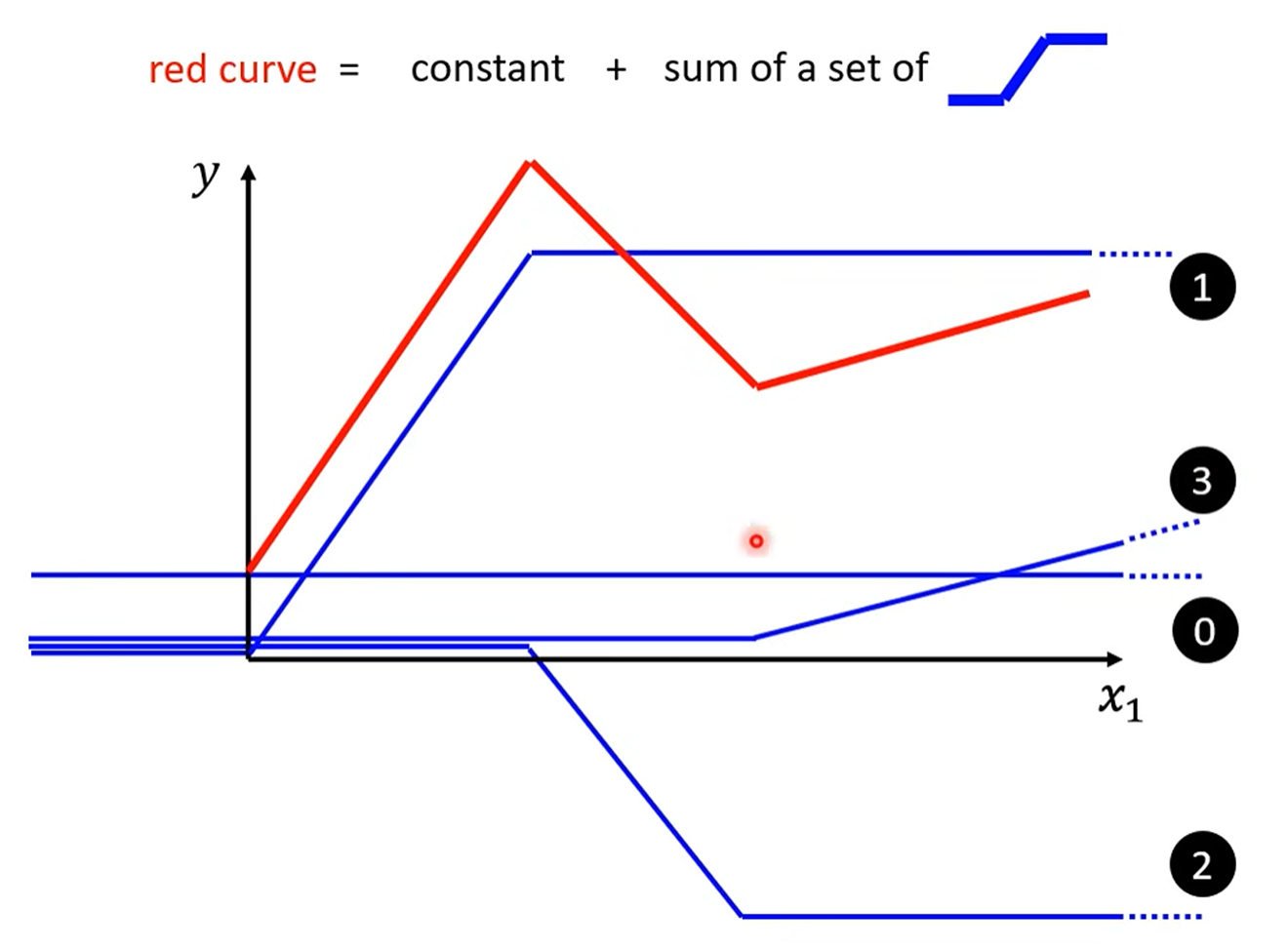
分段线性曲线 (Piecewise Linear Curves):任何复杂的连续曲线,都可以通过足够多的微小线段来逼近。
“蓝色函数” (Hard Sigmoid):这些微小的线段,可以由一种阶梯状的函数(视频中称为“蓝色函数”)来组合而成。
Sigmoid 函数:在数学上,我们可以用一个更平滑、更易于处理的函数——Sigmoid 函数——来近似这个“蓝色函数”。
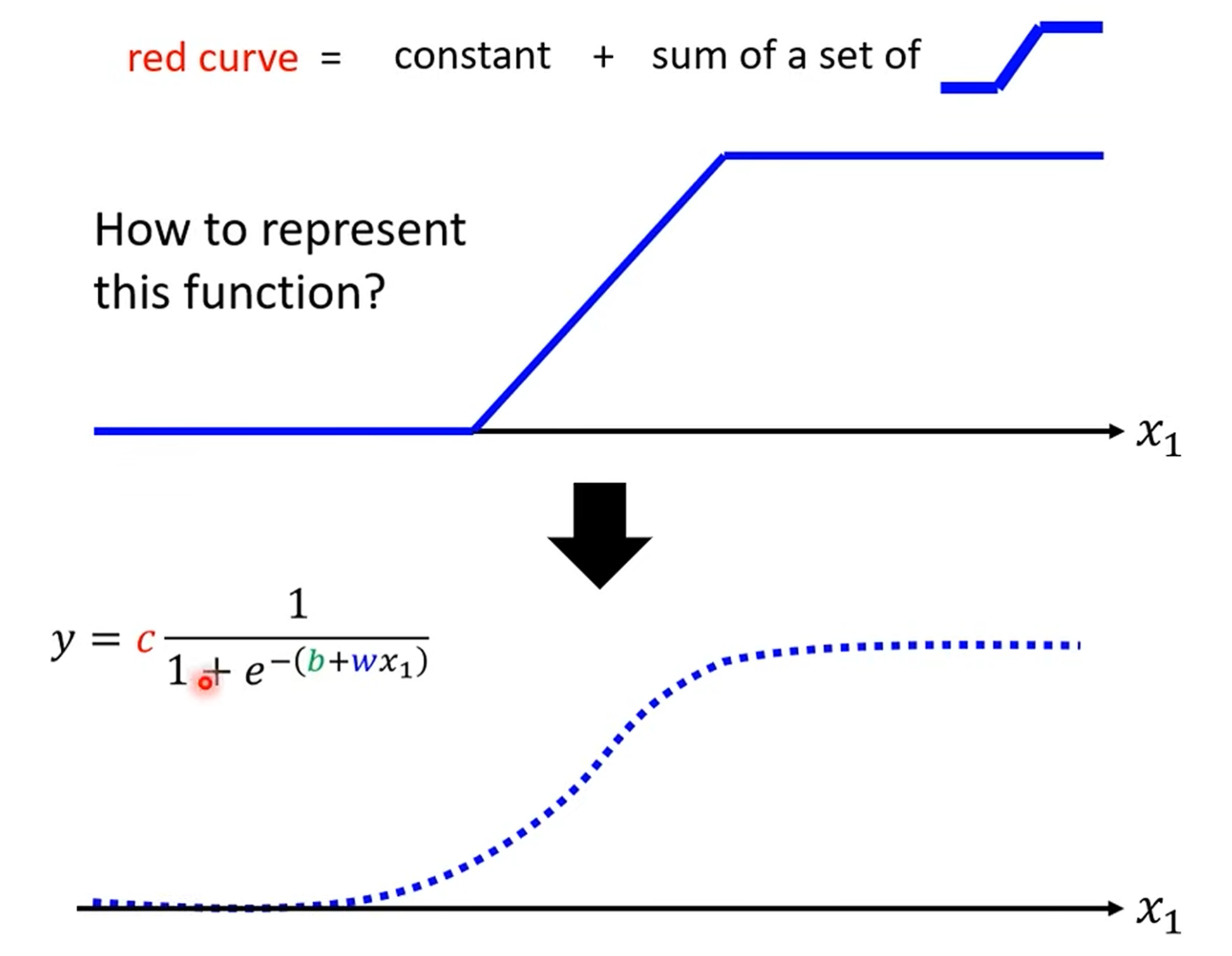
通过调整 Sigmoid 函数的参数(w, b, c),我们可以改变它的形状、位置和高度,从而组合出任意复杂的曲线,以此来逼近我们想要的目标函数。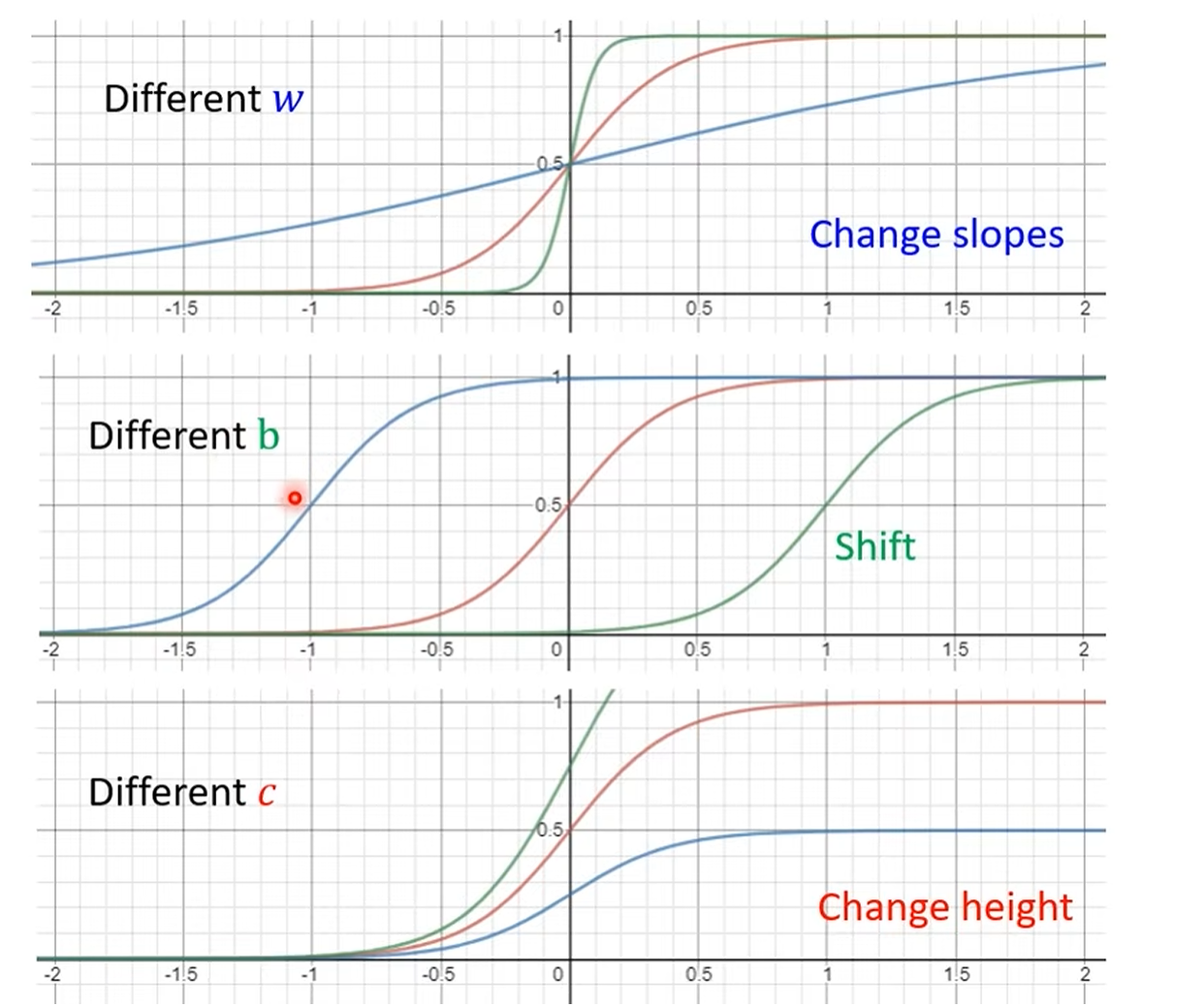
linear model到Curve:

多个features
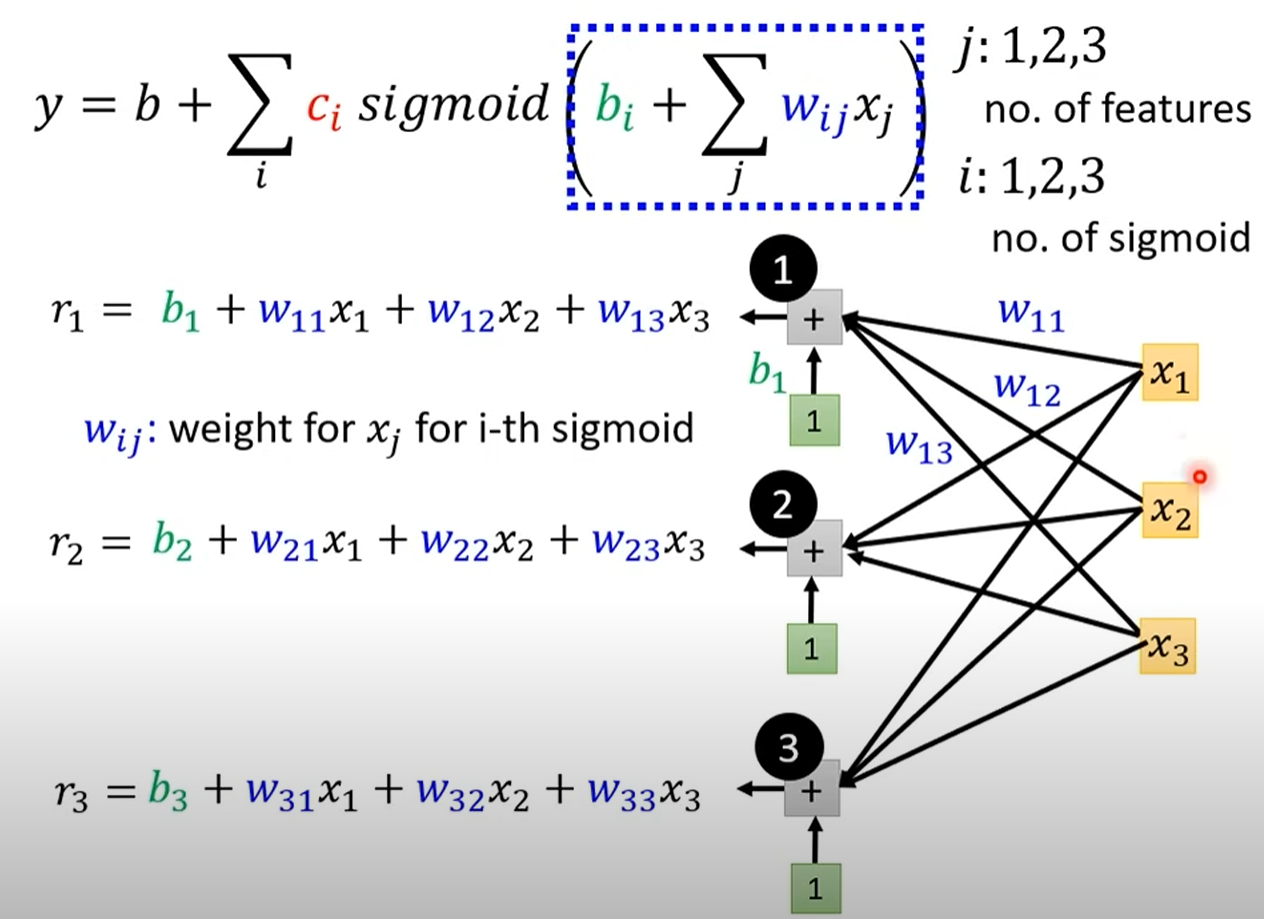
线性代数表示
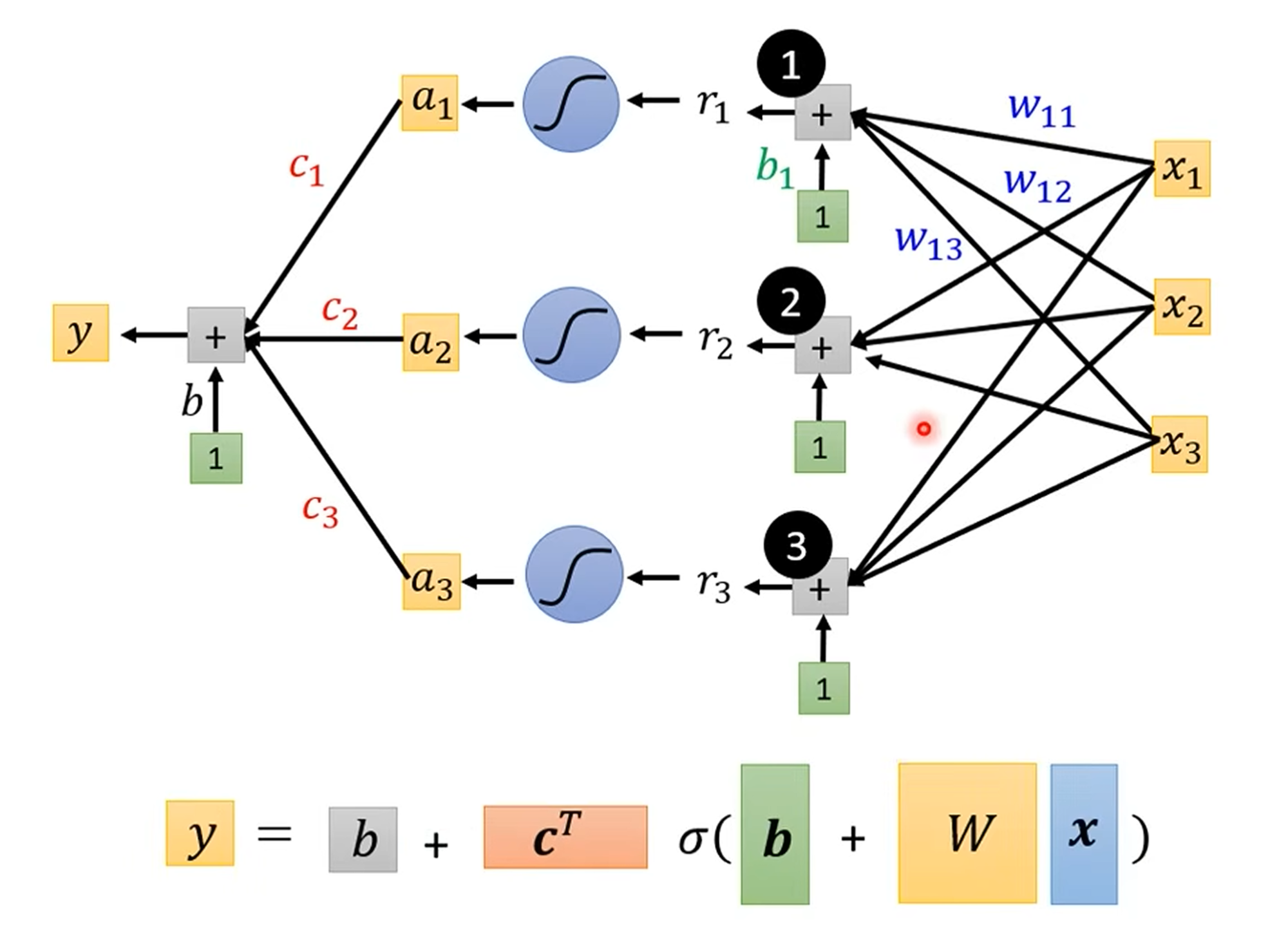
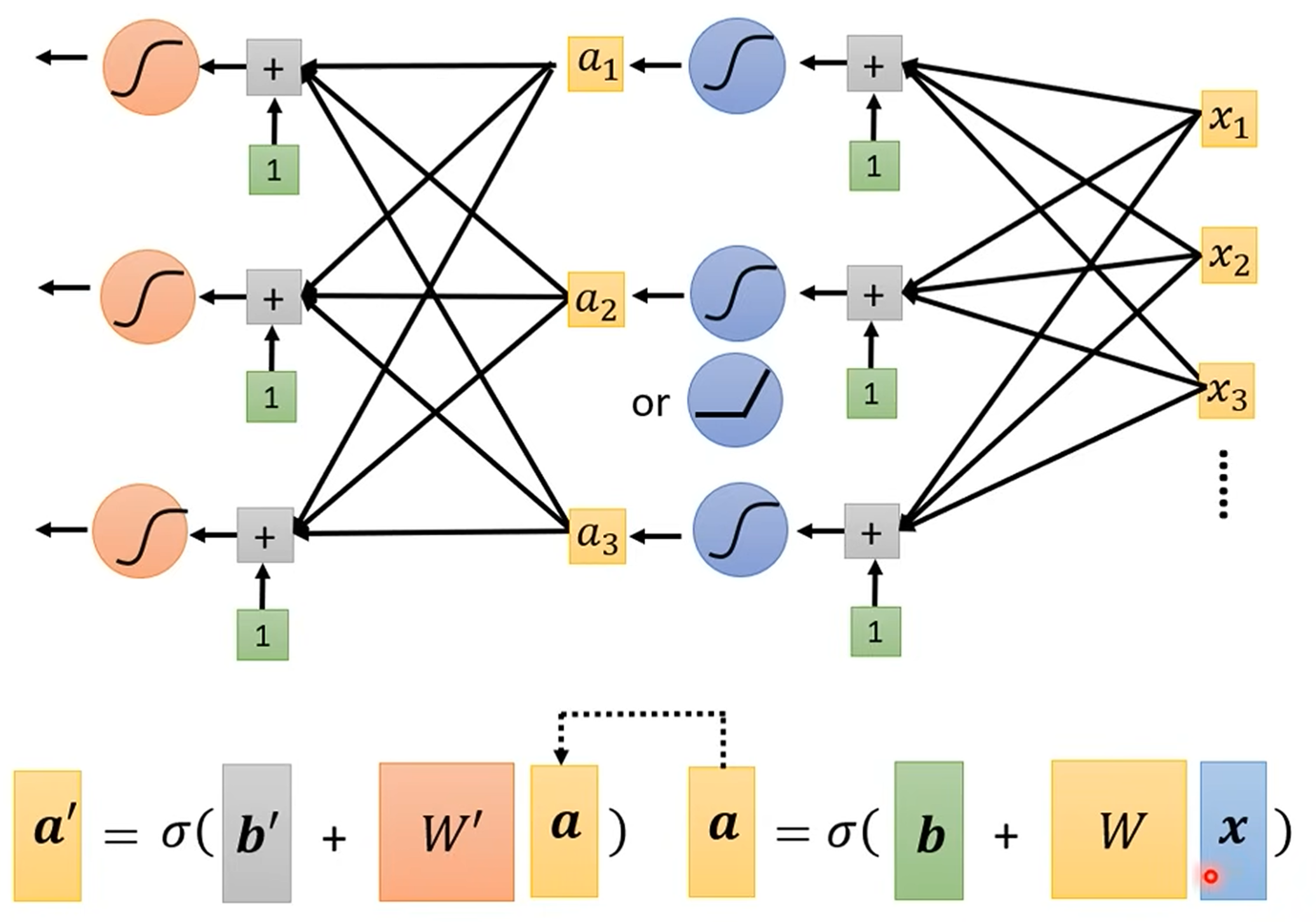
从单个特征到多个特征:神经网络的雏形
当我们的输入不再是单一的“前一天观看人数”,而是包含前7天、前28天等多个特征(features)时,模型也需要相应地升级。
模型结构:
输入层 (Input Layer):接收所有的输入特征
x。隐藏层 (Hidden Layer):每个 Sigmoid 函数(现在被称为“神经元” Neuron)接收所有输入特征的加权和,并经过激活函数(Sigmoid)处理,得到一个激活值
a。输出层 (Output Layer):将所有隐藏层神经元的输出
a进行加权求和,最终得到预测结果y。
数学表示:这个过程可以通过矩阵和向量运算高效地完成,所有的未知参数(权重
w和偏置b)可以被整合到一个大的参数向量θ中。
训练神经网络:同样的配方,更强的模型
尽管模型变得复杂了,但训练它的核心思想依然是我们熟悉的老朋友:
损失函数 (Loss Function):和之前一样,我们定义一个损失函数
L(θ)来衡量模型预测值与真实值之间的差距。优化 (Optimization):我们依然使用梯度下降 (Gradient Descent) 算法来寻找使损失最小化的最佳参数
θ。通过计算损失函数对每一个参数的偏导数(梯度),来指导参数的更新方向。
训练中的实用技巧
Batch 与 Epoch:在实际训练中,我们通常不会一次性将所有数据都用于计算梯度。而是将数据分成一小批一小批(Batch),每次只用一个 Batch 的数据来更新一次参数。当所有 Batch 的数据都被使用过一次后,就完成了一个Epoch。
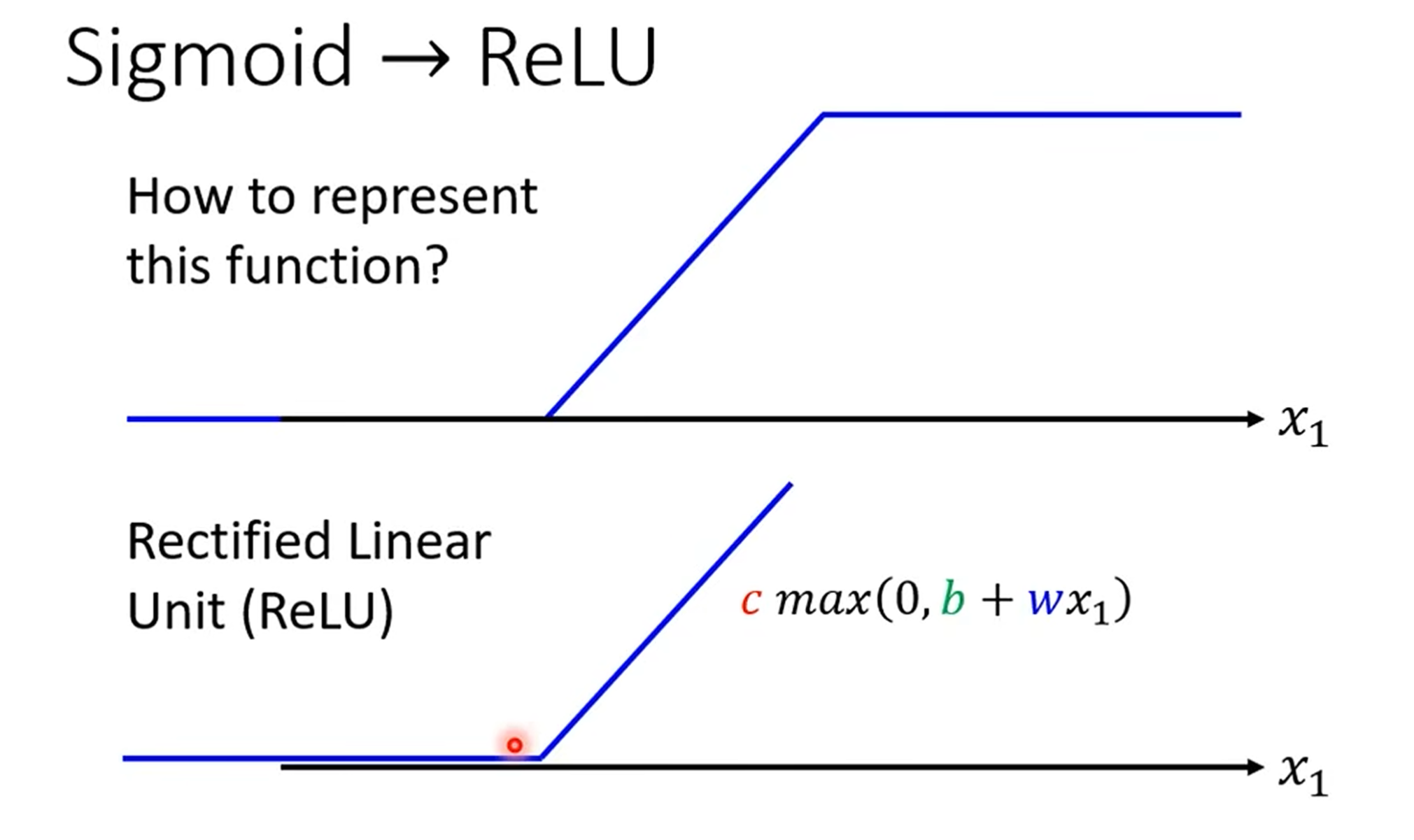
激活函数 (Activation Function):除了 Sigmoid,ReLU (Rectified Linear Unit) 是另一个非常流行且有效的激活函数。它的形式更简单
max(0, x),并且在实践中往往能取得更好的效果。
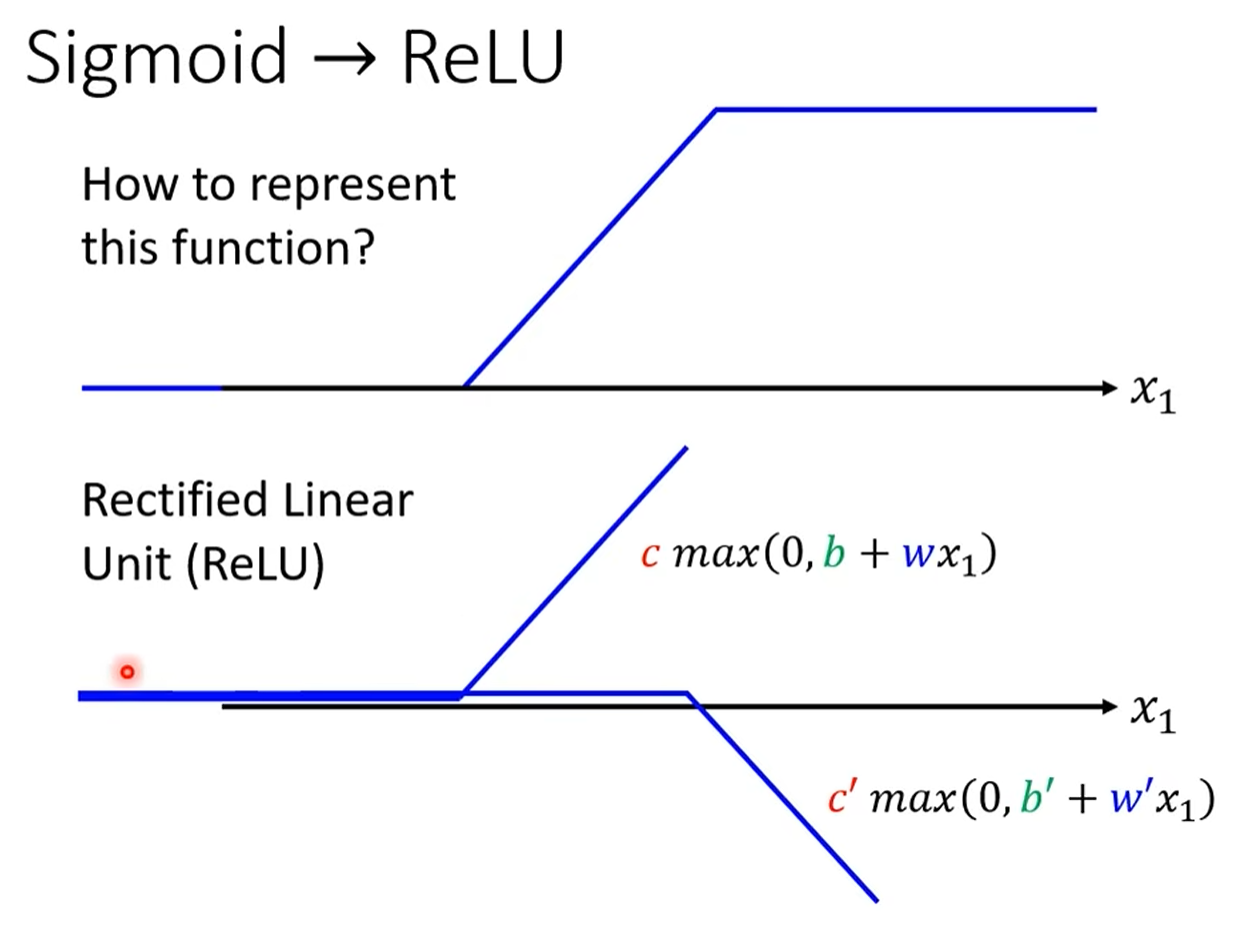
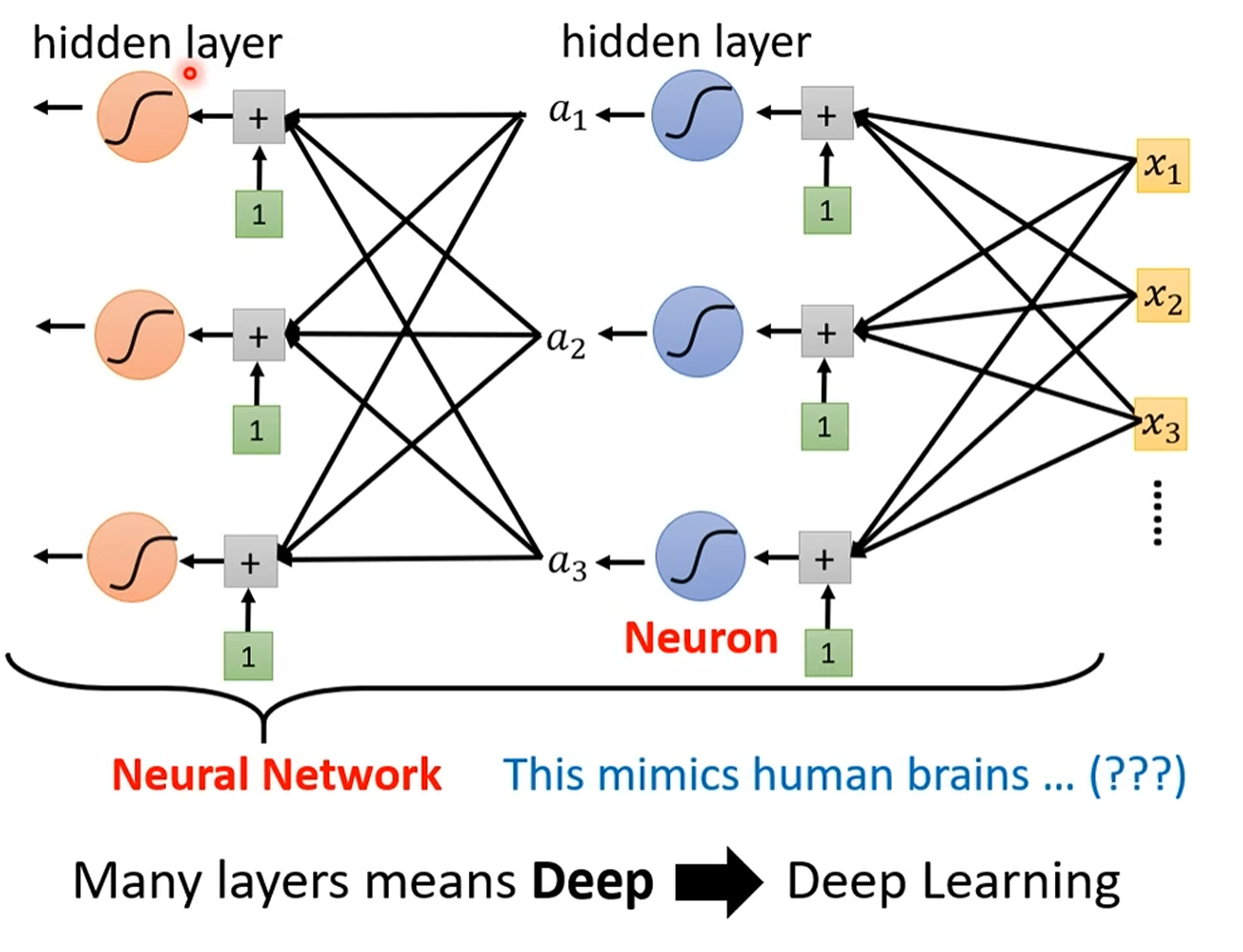
深度学习 (Deep Learning) 的诞生
- “深度”的含义:当我们将多个隐藏层堆叠在一起时,就构成了“深度”神经网络。这就是**深度学习(Deep Learning)**名字的由来。
层数:2
参数更多了:b和b‘,w和w’均是不同的参数
Neuron:sigmoid和ReLu
- 过拟合 (Overfitting):实验结果显示,增加模型的深度(层数)和宽度(每层的神经元数量)可以降低在训练数据上的损失。但并非越深越好,过深的网络可能会导致过拟合——即模型在训练数据上表现完美,但在未见过的测试数据上表现很差。
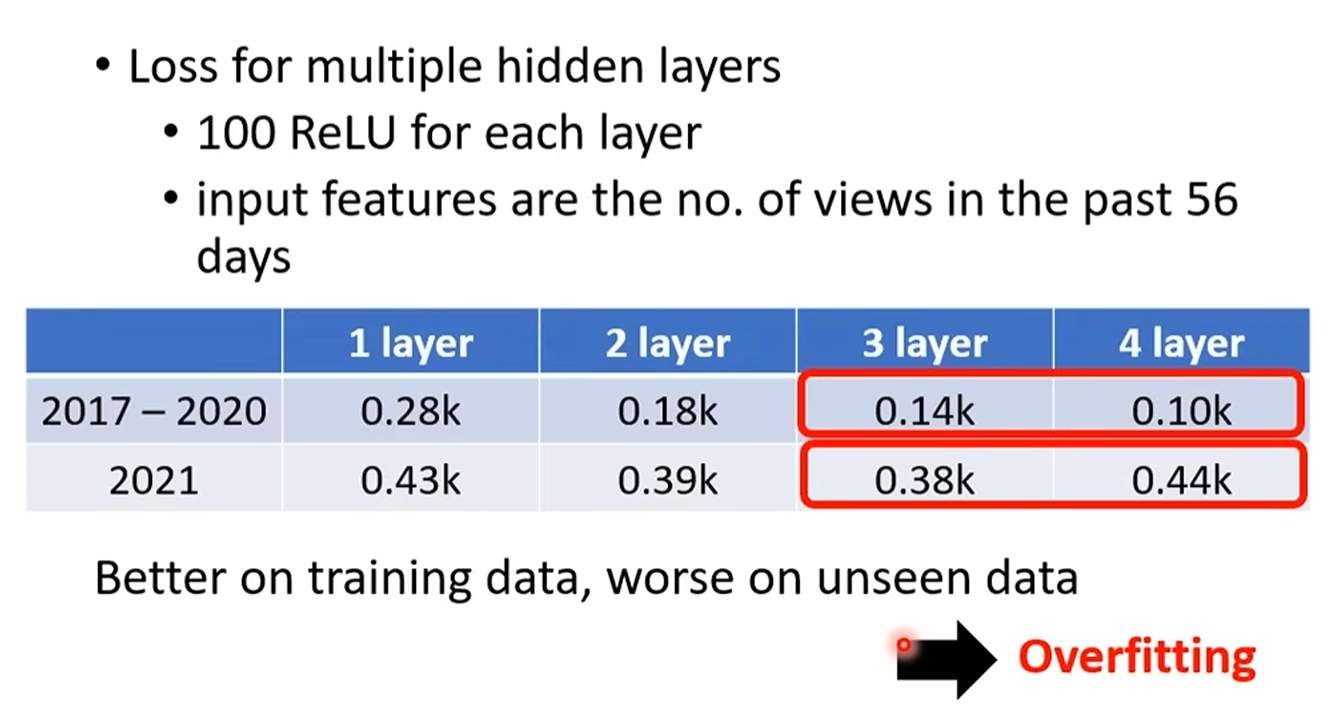
- 核心问题:为什么我们需要“深”而不是仅仅“宽”?课程最后留下了这个引人深思的问题,也为后续更深入的探讨埋下了伏笔。
总结与复习要点
本节课我们完成了从线性模型到非线性模型,再到深度神经网络的认知飞跃。
核心痛点:线性模型的“模型偏见”使其无法处理复杂任务。
核心思想:通过 Sigmoid 或 ReLU 等激活函数,我们可以构建出能够逼近任意复杂函数的神经网络。
核心挑战:模型变得强大的同时,也带来了新的问题,如“过拟合”。如何在模型复杂度和泛化能力之间找到平衡,是深度学习中的一个永恒主题。
