Gradient Descent ,Stochastic Gradient Descent 和Adaptive Moment Estimation
Gradient Descent
我们来一步一步推导前两轮(epoch)梯度下降更新过程,以你提供的代码为基础,展示每轮如何更新参数
$$
初始化:
θ_0=0 \quad
θ_1=0
每个样本的损失函数为:
对参数求导得:
GD:
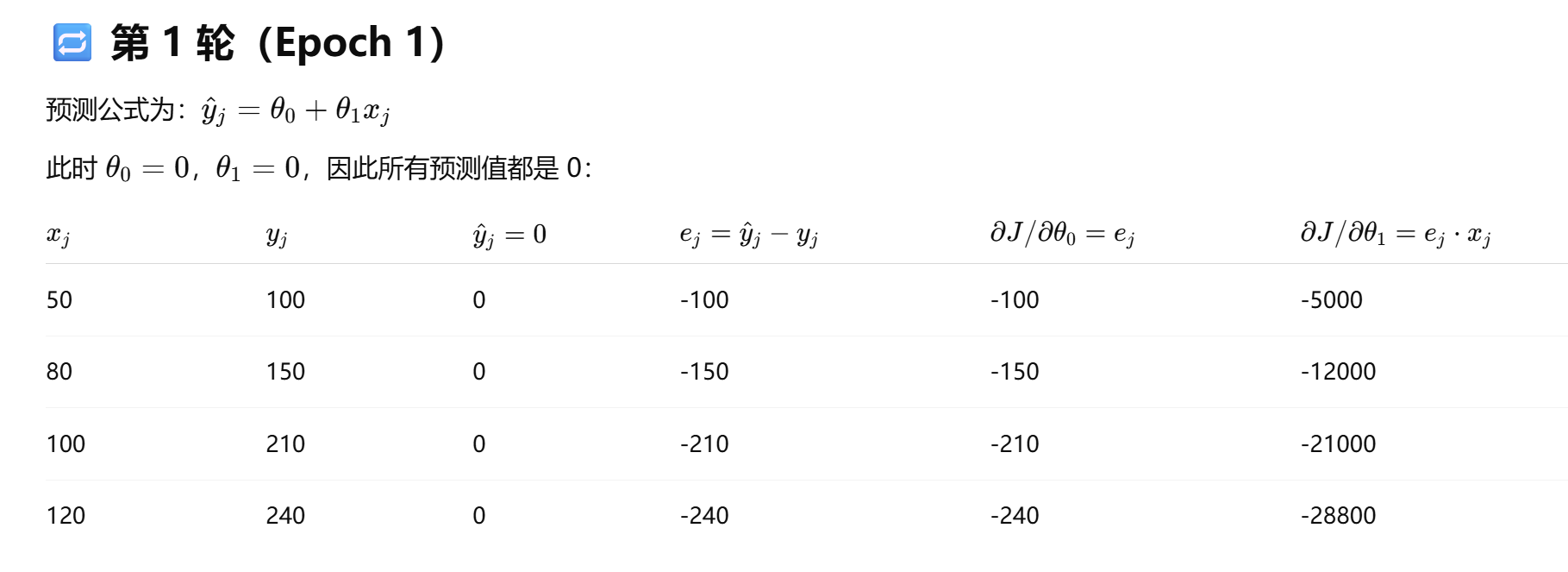

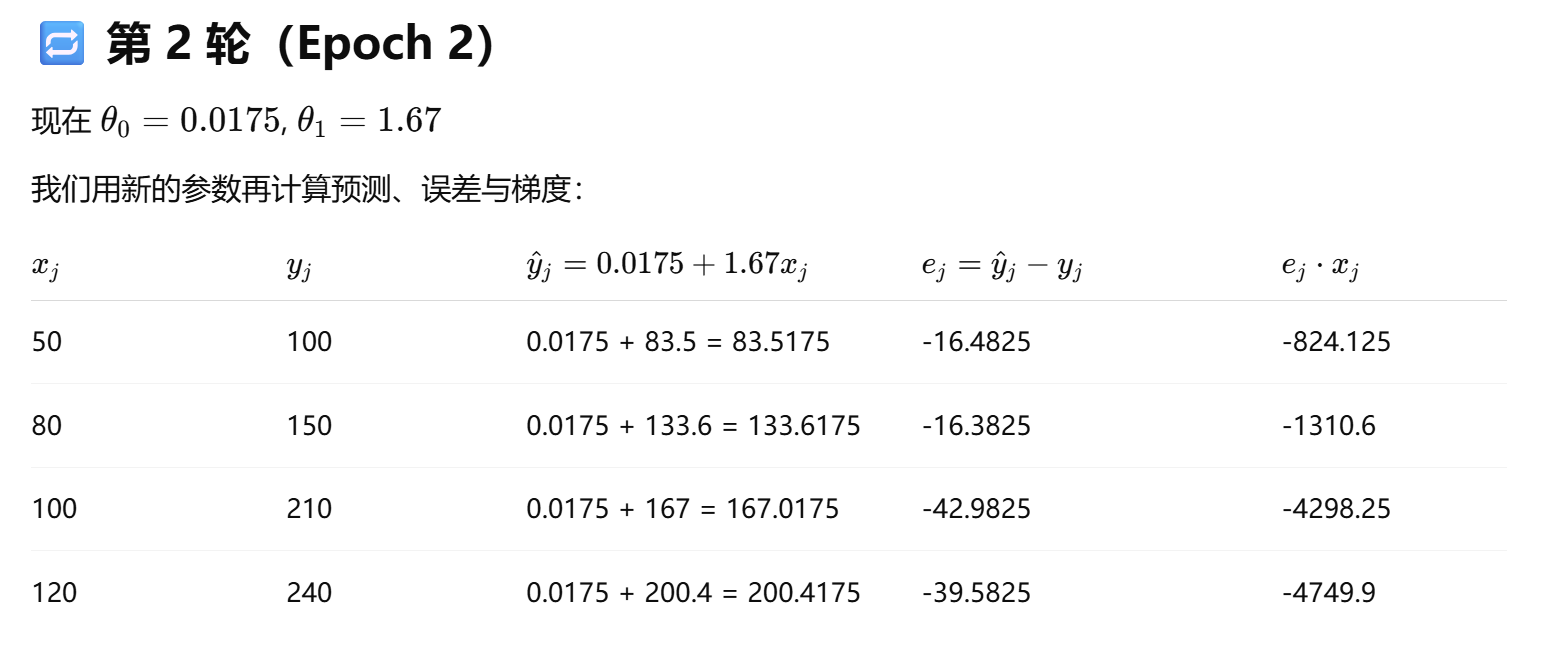

Stochastic Gradient Descent
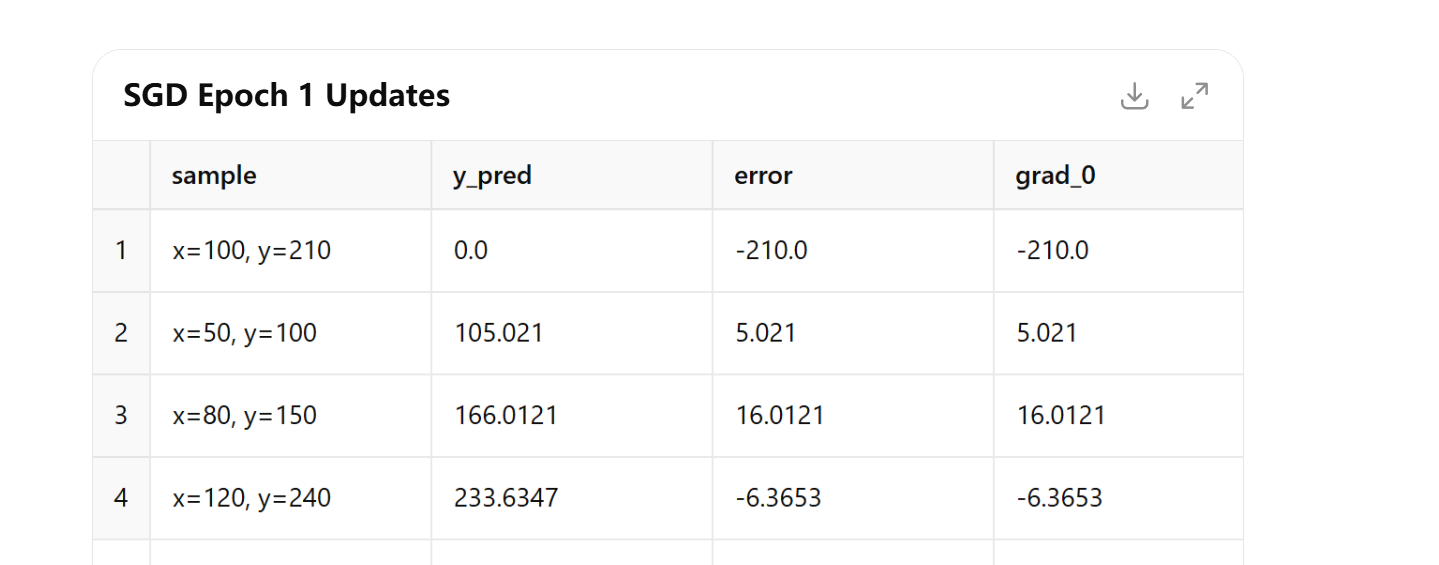
SGD 省略了因子 2,直接用:
每个样本更新时立即使用该梯度进行参数调整:
Adaptive Moment Estimation
Adam = 动量 + 自适应学习率
Adam 优化器非常聪明地将这两个想法结合了起来。它同时做了两件事:
- 它像 Momentum 一样,计算梯度的一阶矩估计(就是梯度的平均值,可以理解为速度)。
- 它像 RMSProp 一样,计算梯度的二阶矩估计(就是梯度平方的平均值,可以理解为颠簸程度或速度的变化)。
然后,它用这两个值来动态地、为每一个参数计算出独立的、最合适的更新步长。
最终效果:Adam 这辆智能小车,既有方向感(动量),又能感知地形(自适应学习率),所以它在绝大多数情况下都能又快又稳地找到山谷的最低点。
Warm Restarts (in SGD) 热重启
这是一种学习率调整策略,全称是 Stochastic Gradient Descent with Warm Restarts (SGDR)。传统的学习率调整策略通常是单调递减的。而 Warm Restarts 策略则是周期性地“重启”学习率。
具体来说,学习率会从一个较高的初始值开始,按照一个预设的函数(如余弦函数)逐渐下降。当下降到最低点后,它会突然被重置回较高的初始值,然后开始下一轮的下降。这个过程就像在模型训练陷入一个局部最优点时,通过突然增大学习率来“踢它一脚”,帮助它跳出当前的局部最小值,去探索更广阔的参数空间,从而有机会找到一个更好的全局最优解。
GA遗传算法
场景:小偷的烦恼
想象一个小偷进入一个珠宝店,他有一个背包,最大承重是 10 公斤。店里有四件宝物,每件宝物的重量和价值如下:
| 宝物 | 重量 (kg) | 价值 (元) |
|---|---|---|
| A (钻石) | 5 | 12 |
| B (黄金) | 4 | 10 |
| C (画作) | 3 | 8 |
| D (花瓶) | 2 | 5 |
目标: 小偷应该如何选择宝物放入背包,才能在不超过背包承重(10kg)的前提下,让总价值最高?
这个问题如果用暴力破解,需要计算 24=16 种组合。当宝物有几十件时,暴力破解就不可行了。这时,遗传算法就派上用场了。
遗传算法的解决步骤
第1步:基因编码 (Encoding)
首先,我们需要把一个“解决方案”(即一种拿宝物的组合)表示成一串“基因”,也就是染色体 (Chromosome)。
最简单的方法是用一个长度为4的二进制字符串,每一位对应一件宝物。
1代表“拿这件宝物”0代表“不拿这件宝物”
例如:
[1, 0, 1, 0]代表:拿A(钻石)和C(画作),不拿B和D。[0, 1, 1, 1]代表:拿B(黄金)、C(画作)和D(花瓶)。
第2步:初始化种群 (Initialization)
遗传算法不是从一个解开始,而是从一个种群 (Population) 开始。我们随机生成一组初始的染色体(解决方案)。假设我们随机生成了下面4个个体组成了我们的初始种群:
个体1:
[1, 1, 0, 0]个体2:
[0, 1, 1, 1]个体3:
[1, 0, 1, 0]个体4:
[0, 0, 1, 1]
第3步:适应度评估 (Fitness Evaluation)
现在,我们需要一个函数来评估每个个体(解决方案)的好坏,这就是适应度函数 (Fitness Function)。
在这个问题里,适应度就是所选宝物的总价值。但有一个关键规则:
如果总重量超过背包承重(10kg),那么这个方案是无效的,适应度为 0。
我们来计算一下初始种群的适应度:
个体1
[1,1,0,0]:重量: 5 + 4 = 9kg (≤ 10kg) -> 有效
价值: 12 + 10 = 22
适应度 = 22
个体2
[0,1,1,1]:重量: 4 + 3 + 2 = 9kg (≤ 10kg) -> 有效
价值: 10 + 8 + 5 = 23
适应度 = 23
个体3
[1,0,1,0]:重量: 5 + 3 = 8kg (≤ 10kg) -> 有效
价值: 12 + 8 = 20
适应度 = 20
个体4
[0,0,1,1]:重量: 3 + 2 = 5kg (≤ 10kg) -> 有效
价值: 8 + 5 = 13
适应度 = 13
目前来看,个体2 [0,1,1,1] 是当前种群中最好的解决方案。
第4步:选择 (Selection)
遵循“优胜劣汰”的自然法则,适应度越高的个体,越有可能被选中作为“父母”来繁衍下一代。
常见的选择方法是轮盘赌选择法。想象一个轮盘,每个个体的扇区大小与它的适应度成正比。适应度为23的个体2,扇区最大,最容易被指针选到。
假设经过选择,我们选中了个体2和个体1作为父母进行繁殖。
第5步:交叉 (Crossover)
交叉是模拟生物繁殖,父母双方交换部分基因,产生全新的后代。
我们随机选择一个交叉点,比如在第2位基因后面。然后将两个父代染色体的后半部分进行交换。
父代1:
[0, 1 | 1, 1](来自个体2)父代2:
[1, 1 | 0, 0](来自个体1)
交换|后面的部分,产生两个新的子代:
子代1:
[0, 1, 0, 0]子代2:
[1, 1, 1, 1]
第6步:变异 (Mutation)
为了防止算法陷入局部最优(比如所有个体都长得差不多),我们需要引入变异,以一个很小的概率随机改变基因。
比如,我们对子代1进行变异:
变异前:
[0, 1, 0, 0]随机选择第4位进行变异(0 -> 1)
变异后:
[0, 1, 0, 1]
这个变异后的新个体 [0,1,0,1] 代表拿B和D,总重6kg,价值15,这是一个全新的、可能不错的解决方案!
第7步:新一代与循环
通过交叉和变异产生的新个体(子代)将组成新一代的种群。然后,算法回到第3步(适应度评估),对新种群进行评估,然后再次进行选择、交叉、变异。
这个过程周而复始,一代又一代地“进化”。
最终结果
经过很多代的进化后,种群中适应度最高的个体将趋于稳定。最终,算法可能会收敛到 [0,1,1,1] (价值23) 或者 [1,1,0,0] (价值22) 或者其他更好的解。在这个简单例子里,最优解就是 [0,1,1,1],总价值23。遗传算法通过模仿进化,很有可能找到这个最优解。
AHP和TOPSIS
- AHP 是基于人的主观判断,核心在于“比较重要性”,强调结构化思考 + 权重提取;
- TOPSIS 是基于数据的客观距离计算,核心在于“谁更接近理想”,强调最优解的几何逼近。
| 维度 | AHP(层次分析法) | TOPSIS(理想解法) |
|---|---|---|
| 输入依赖 | 依赖专家主观判断(两两比较) | 依赖方案原始数据矩阵(如成本、评分等) |
| 核心思想 | 通过成对比较提取每个准则的重要性权重 | 选出离正理想解最近、离负理想解最远的方案 |
| 数学依据 | 特征值理论(判断矩阵的主特征向量) | 欧几里得距离(几何空间距离) |
| 输出结果 | 准则权重、方案得分 | 方案的贴近度 Ci,排序 |
| 数据需求 | 需要构建判断矩阵,规模太大效率低 | 只需标准化原始数据,不需要主观比较 |
| 一致性检验 | 需进行一致性比率 CR 检验 | 不需要一致性检验 |
| 适用场景 | 人工可比主观偏好强的情境(战略、政策等) | 有客观指标、数据齐全,需数值化评估的情境(选产品) |
| 优点 | 可量化主观偏好,结构清晰 | 简单直观、计算快速,适用性广 |
| 缺点 | 主观性强,维度多时构建判断矩阵困难 | 忽略指标之间可能的权重差异或相关性 |
TOPSIS(原始决策矩阵+每个指标的权重)
返回参数的排序
| 方案 | 价格(万元) | 性能(分) | 重量(kg) | 续航(小时) |
|---|---|---|---|---|
| A | 5 | 80 | 1.5 | 8 |
| B | 6 | 90 | 1.2 | 10 |
| C | 4.5 | 70 | 1.8 | 6 |
| 这反映了决策者对各个指标“重要程度”的主观或客观判断: |
权重向量
比如:
- 价格 0.3(越低越好)
- 性能 0.4(越高越好)
- 重量 0.1(越低越好)
- 续航 0.2(越高越好)
