MLP

2025-08-26

9k 词

在 Embedding 里 `dim` 的意思

dim 表示你操作的 维度索引。
张量有很多维度（axis），dim 决定了你在哪个维度上做操作。

举例：

1	emb.shape = (32, 3, 2)

这里 3 个维度的含义分别是：

dim=0 → batch 维度（32 个样本）
dim=1 → 序列长度（每个样本 3 个索引）
dim=2 → embedding 向量维度（每个索引是 2 维）

Embedding 查表 (Embedding Lookup)

思路拆解

X 的形状
- X.shape = (32, 3)
- 含义：一共有 32 个样本（batch），每个样本里面有 3 个索引。
C 的形状
- C.shape = (27, 2)
- 含义：这是一个查找表（embedding table），一共有 27 行，每行是 2 维向量。
C[X] 的运算
- 对每个 X[i, j]，用它作为索引，去 C 里取对应的那一行（形状 (2,)）。
- 所以一行 X [a, b, c] 会变成 C[[a, b, c]]，形状 (3, 2)。
- 整个 32 个样本就堆叠起来，得到 (32, 3, 2)。

公式

$'_' allowed only in math mode\text{shape}(C[X]) = \text{shape}(X) + \text{embedding_dim}$

在你的例子里：

(32,3)+(2,)=(32,3,2)(32, 3) + (2,) = (32, 3, 2)

拼接方式

1. 展平（flatten）

最高效的拼接方法

1	emb.view(32, 6)

因为 (32, 3, 2) 可以理解为 3×2=6，所以把最后两维拼起来，得到

1	emb.view(32, 6).shape = (32, 6)

每个样本的 embedding 被拉平成一个长度为 6 的向量。

2.手动切片再拼接

1	torch.cat([emb[:, 0, :], emb[:, 1, :], emb[:, 2, :]], dim=1)

emb[:, 0, :] → (32, 2)
emb[:, 1, :] → (32, 2)
emb[:, 2, :] → (32, 2)
拼接后 (32, 6)。

3.利用 unbind

1	torch.cat(torch.unbind(emb, dim=1), dim=1)

torch.unbind(emb, dim=1) 会把第 1 维（长度=3）拆开 → 得到 3 个 (32, 2) 张量
再 torch.cat(..., dim=1) 拼接 → (32, 6)

两种方法都是 把 (32,3,2) 转成 (32,6)，本质上等价于 emb.view(32,6)。

项目拆解：

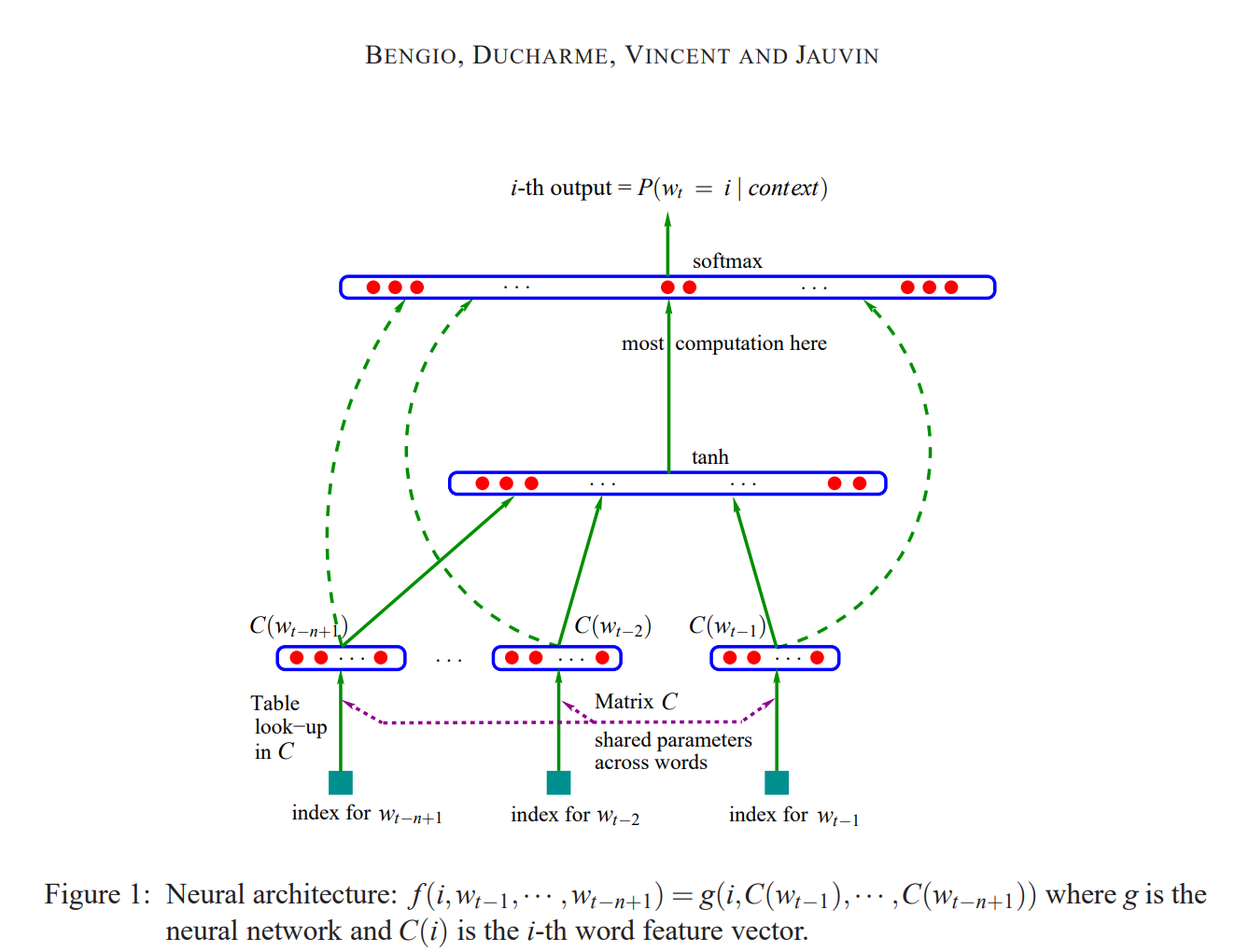
模型的输入和输出维度是变化的，我们来一步步拆解一下。

简单来说，可以把数据在网络中的流动想象成一个工厂流水线，原材料（输入）在每个工位（网络层）都会被加工，其“形状”（维度）也会随之改变。

我们用视频中的具体例子来解释：

batch_size (批量大小) = 32
block_size (上下文长度) = 3
embedding_dim (嵌入向量维度) = 10
vocab_size (词汇表大小) = 27
hidden_size (隐藏层神经元数量) = 200

输入 (Input) 的维度变化

输入的处理过程主要有三步，每一步的维度都不同：

最原始的输入 X：(32, 3)
- 维度: (batch_size, block_size)
- 解释: 这是我们喂给模型的第一批原始数据。它是一个整数张量（Tensor）。每一行是一个训练样本（共32个），每一行中的3个数字是构成上下文的3个字符的索引（例如，[5, 13, 13] 代表 ‘e’, ‘m’, ‘m’）。此时，数据还没有“特征”的概念，只是代表字符的编号。
经过嵌入层后的输入 emb：(32, 3, 10)
- 维度: (batch_size, block_size, embedding_dim)
- 解释: 这是真正进入神经网络计算的特征。模型通过一个查找表 C（形状为 (27, 10)），将上一步的每个字符索引（如 5）都转换成了一个10维的特征向量（词嵌入）。所以，原来 (32, 3) 的索引矩阵，就变成了 (32, 3, 10) 的浮点数特征矩阵。现在每一行代表一个样本，每个样本包含3个10维的向量。
展平（Flatten）后的输入：(32, 30)
- 维度: (batch_size, block_size * embedding_dim)
- 解释: 全连接的隐藏层（Linear Layer）无法直接处理 (32, 3, 10) 这样的三维输入。它需要一个二维的矩阵，形状为 (批量大小, 特征数量)。因此，我们需要将每个样本的3个10维向量拼接成一个单一的30维向量。这一步就是通过 torch.view 操作完成的。view(32, 30) 将 (32, 3, 10) 的数据“压平”成了 (32, 30)。这才是隐藏层接收到的最终输入。

输出 (Output) 的维度

网络的最终输出，我们只关心其预测结果的维度。

最终输出 logits：(32, 27)
- 维度: (batch_size, vocab_size)
- 解释: 经过隐藏层（输出 (32, 200)）和最后的输出层之后，模型为我们批量中的每一个样本（共32个），都生成了一个包含27个数值的向量。
- 这27个数值就是 logits（原始得分），分别对应着字母表中下一个字符可能是’a’到’z’以及特殊字符’.’的概率得分。这个得分越高，代表模型认为该字符是下一个正确字符的可能性越大。
- 这个 (32, 27) 的输出会和我们的目标标签 Y（一个形状为 (32,) 的整数向量，包含了32个样本的正确答案索引）一起被送入 F.cross_entropy 损失函数中，用于计算损失并进行反向传播。

完整流程：

1. 输入：确实是一整个“批次”的“索引矩阵”

我们不是一个一个字符地输入，也不是一个一个样本（一组上下文）地输入，而是一次性输入一个**批次（batch）**的数据。

输入 X 的形状是 (32, 3)：这代表我们一次性处理 32个不同的训练样本。
每个样本的维度是 3：这 3 个数字就是您说的“拼接好的字符索引”，也就是上下文窗口（block_size）中的3个字符在词汇表里的编号。

2. Embedding层：学习“关系”的压缩空间

查找与转换：模型接收到 (32, 3) 的索引后，会去一个叫做 C 的大矩阵（图中的 “Matrix C”）里查找。这个 C 的形状是 (27, 10)，相当于一张有27行、10列的表格。
学习相似性：输入的每个索引（比如5）就对应表格中的某一行（第5行），这一行就是一个10维的向量。在训练过程中，模型会不断调整这个 C 矩阵里的值，使得功能或意义上相似的字符（比如所有的元音字母）它们的向量在10维空间里的位置会变得越来越接近。

3. 展平（Flatten）：为隐藏层准备“标准格式”的输入

经过 Embedding 后，我们的数据形状从 (32, 3) 变成了 (32, 3, 10)。
但是，标准的全连接隐藏层（图中标着 tanh 的那一层）只能接收一个二维矩阵 (样本数, 特征数)。
因此，我们必须把每个样本的 (3, 10) 这部分“铺平”，也就是将3个10维的向量拼接成1个30维的长向量。这样数据形状就从 (32, 3, 10) 变成了 (32, 30)，完美地符合了隐藏层的输入要求。

4. 输出层：一个需要 уточнение (clarification) 的小细节

隐藏层激活 (tanh)：数据 (32, 30) 进入隐藏层，经过线性变换后，使用 tanh 函数进行激活。tanh 是作用在隐藏层的。
输出层 (Logits)：tanh 的输出结果，再进入下一个线性层（图中最上面的蓝色粗框），计算出最终的得分（logits）。这个输出的形状是 (32, 27)。
概率转换 (softmax)：最后一步，才是将这个 (32, 27) 的得分矩阵通过 softmax 函数，转换成概率分布。softmax 是作用在最终输出层之后，用来解释结果的。

流程是： 展平 -> 隐藏层线性变换 -> tanh 激活 -> 输出层线性变换 -> softmax。

Pytorch的强大之处-Fused Kernel：

Fused Kernel（融合计算核心） 是现代深度学习框架（如PyTorch, TensorFlow）和硬件（GPU）中一个至关重要的性能优化技术。

厨房的比喻

非融合操作 (Non-Fused Operation)：

想象一下你在厨房做一道菜，需要三个步骤：1.切菜，2.炒菜，3.装盘。

你先把所有菜都切好，然后把它们全部放回冰箱（慢速内存）。接着，你再从冰箱里把切好的菜拿出来，开始炒菜，炒好后又全部放回冰箱。最后，你再从冰箱里把炒好的菜拿出来，开始装盘。

在这个过程中，你来回开关冰箱、存取食材花费了大量的时间。
融合操作 (Fused Operation / Fused Kernel)：

现在，你把需要处理的菜放在手边的操作台（快速缓存/寄存器）上。你直接在操作台上完成切菜、炒菜，然后立刻装盘。整个过程一气呵成，几乎没有浪费时间去冰箱存取半成品。

Fused Kernel 的技术解释

在GPU计算中，“冰箱”就是速度较慢的全局内存（Global Memory），“操作台”就是速度极快的片上缓存或寄存器（On-chip Cache/Registers）。

Kernel (计算核心)：

一个 “Kernel” 是指发送给GPU执行的一个独立的计算任务。例如，torch.exp(x) 会启动一个指数运算的Kernel，torch.sum(y) 会启动一个求和的Kernel。
Fused Kernel (融合计算核心)：

它指的是将多个独立的、连续的计算步骤（Kernels）合并成一个单一的、更大的Kernel。

F.cross_entropy 这个函数就是使用了 Fused Kernel。我们来看看它融合了哪些操作：

如果不使用 Fused Kernel，手动计算交叉熵损失需要以下步骤：

logits -> Softmax

a. 对 logits 取指数 torch.exp() (启动第1个Kernel，生成一个中间结果)

b. 对指数结果按行求和 torch.sum() (启动第2个Kernel，又一个中间结果)

c. 用指数结果除以和 a / b (启动第3个Kernel，得到概率 probs)
probs -> Negative Log Likelihood Loss

d. 对概率 probs 取对数 torch.log() (启动第4个Kernel，又一个中间结果)

e. 根据正确标签 y 提取对应的对数概率 (启动第5个Kernel)

f. 取负数并求平均值 (启动第6个Kernel)

你看，这个过程不仅繁琐，而且每一步都会产生一个巨大的中间张量（比如 probs），这些张量需要被写入GPU的全局内存，然后在下一步再被读取出来。这种频繁的内存读写是非常耗时的。

使用 F.cross_entropy (Fused Kernel) 的情况：

你只需要调用一个函数，它会启动一个高度优化的 Kernel。这个Kernel在GPU内部，一口气完成上述所有的计算步骤。中间结果（如probs）尽可能地被保留在超高速的片上缓存中，而不需要写入慢速的全局内存。

Fused Kernel 的三大优势

大幅减少内存读写 (Drastically Reduces Memory I/O)：这是最核心的优势。避免了生成和存储多个巨大的中间张量，从而显著减少了对慢速全局内存的访问次数，极大提升了计算速度。
减少计算启动开销 (Reduces Kernel Launch Overhead)：CPU每次命令GPU启动一个Kernel都有微小的开销。启动1个大Kernel比启动6个小Kernel的总体开销要小得多。
提升数值稳定性 (Improves Numerical Stability)：这也是视频中提到的关键点。在计算 exp(logits) 时，如果 logits 中的数值很大，结果可能会溢出变成 inf（无穷大），导致计算错误。融合后的Kernel可以使用一些数学技巧（如 Log-Sum-Exp Trick）来巧妙地避免这种溢出问题，使得计算在数值上更加稳定和精确。

交叉熵损失（Cross-Entropy Loss）

第一部分：Softmax (从 Logits 到概率)

“把logit进行exp之后，归一化”，这个操作本身就叫 Softmax 函数。

目的：它的唯一目的就是将模型输出的一组任意分值的 logits（例如 [-1.2, 3.4, 0.5]），转换成一个规范的概率分布。
特性：经过 Softmax 处理后，输出的向量有两个特点：
1. 所有元素都在 0 到 1 之间。
2. 所有元素之和等于 1。
结果：这样我们就得到了模型预测的：“下一个字符是’a’的概率是10%，是’b’的概率是85%，是’c’的概率是5%…”

第二部分：负对数似然损失 (Negative Log Likelihood Loss)

后续步骤 “将索引和标签输入概率矩阵，取log，取平均，取负号”，这部分合起来就是负对数似然损失。

挑选正确概率：我们从上面得到的概率分布中，只关心正确答案所对应的那个概率值。比如，如果正确答案是 ‘b’，我们就从 [0.10, 0.85, 0.05] 中挑选出 0.85。
取 Log 再取负号 (-log(p))：这是损失函数的核心。
- 如果模型预测得非常准，正确答案的概率 p 接近 1（比如 0.99），那么 -log(0.99) 是一个非常小的数（接近0）。这意味着损失很小，惩罚很轻。
- 如果模型预测得非常差，正确答案的概率 p 接近 0（比如 0.01），那么 -log(0.01) 是一个非常大的数。这意味着损失很大，惩罚很重。
  
  这个特性完美地符合我们对一个损失函数的要求：预测越差，惩罚越重。
取平均：因为我们一次处理一个批次（batch）的样本（比如32个），我们会为这32个样本分别计算出损失值。最后，我们将这32个损失值加起来求一个平均，得到一个单一的数值，代表模型在这个批次上的总体表现。这个最终的数值就是我们用来进行反向传播、更新模型参数的依据。

minibatch加速

一、为什么需要 Batch？(动机)

想象一下，你的整个训练数据集 X 有20多万个样本。训练模型需要计算损失函数对参数的梯度，以便更新参数。这里有两种极端的做法：

极端一：使用全部数据 (Full Batch)
- 做法：一次性将20多万个样本全部喂给模型，计算一个总损失，然后进行一次反向传播和参数更新。
- 缺点：计算量极其巨大。20多万个样本的前向传播和反向传播可能会耗尽你的内存，而且花费的时间会非常非常长。你可能要等几分钟甚至几小时才能完成一步更新。
极端二：一次只用一个数据 (Stochastic Gradient Descent, SGD)
- 做法：一次只随机取一个样本，计算损失，更新一次参数。
- 缺点：极其不稳定。单个样本带来的梯度具有很大的随机性，可能会让模型的训练过程像喝醉酒一样摇摇晃晃，虽然大方向对，但收敛速度会很慢。同时，这也没有充分利用GPU并行计算的优势。

Minibatch (小批量) 就是介于两者之间的完美平衡点。我们一次取一小撮数据（例如32个），这一小撮数据就称为一个 “minibatch”。

优点：
- 计算高效：32个样本的计算量很小，一步更新非常快。
- 梯度稳定：32个样本的平均梯度比单个样本的梯度要稳定得多，能更准确地指向正确的下降方向。
- 充分利用硬件：可以高效地进行并行计算。

二、代码是怎么实现 Batch 的？(图解)

现在我们来逐行看懂图中# minibatch construct部分的代码，这正是“抓取一小撮数据”的过程。

# 假设 X 的总大小是 (228146, 3)
# 假设 Y 的总大小是 (228146,)

# minibatch construct
ix = torch.randint(0, X.shape[0], (32,))

X.shape[0]: 这是获取我们完整数据集 X 的总样本数，也就是总行数，比如 228146。
torch.randint(0, 228146, (32,)): 这是这行代码的核心。它的意思是：
- 请在一个从 0 到 228145 的整数范围内…
- …随机地、可重复地抽取…
- …32 个整数。
- 执行后，ix 会变成一个包含32个随机数字的张量（Tensor），例如 tensor([501, 189234, 98, ..., 76521])。
ix 现在就是我们这一批（batch）随机选出来的样本的“门牌号”或者说“行索引”。
emb = C[X[ix]] 和 loss = F.cross_entropy(logits, Y[ix])
- X[ix]: 这是利用 ix 来从整个数据集 X 中“取出”数据的关键一步。PyTorch/Numpy允许我们用一个索引列表（或张量）来一次性地选取多行数据。X[ix] 的结果就是一个新的、更小的张量，形状为 (32, 3)。这 32 行数据就是我们本次训练要用的 minibatch。
- Y[ix]: 同理，我们使用完全相同的索引 ix 从标签集 Y 中取出对应的32个正确答案。这保证了数据和标签是一一对应的。

“Learning Rate Range Test”（学习率范围测试）

一、核心思想：为什么学习率如此重要？

首先，我们要理解学习率（Learning Rate, LR）扮演的角色。在梯度下降中，我们计算出让损失（loss）减小的“方向”（梯度），然后沿着这个方向“走一步”来更新模型的参数。

学习率就是你“这一步”迈得有多大（步长）。

学习率太小 (Too Low)：你每一步都迈得小心翼翼，像在挪动。虽然方向是对的，但要走到谷底（损失最低点）会花费极长的时间，训练效率极低。
学习率太大 (Too High)：你每一步都迈得大步流星。你可能一步就直接跨过了谷底，跳到了对面的山坡上。下一步你又想往回走，结果可能又跳了回来。最终结果就是在谷底两侧来回震荡，甚至越跳越远（损失爆炸，变成 NaN），永远无法收敛。

因此，找到一个“不大不小刚刚好”的学习率，是模型训练成功与否的关键。

二、暴力搜索的问题

最朴素的想法是：“我多试几个值不就行了？比如 0.1, 0.01, 0.001…”。

这种方法的问题在于：

盲目：你不知道最佳值到底在哪个数量级，可能试了很多次都错过了最佳范围。
耗时：每次尝试都需要从头开始一次完整的训练，如果模型很大，试一次可能就要几个小时甚至几天，成本太高。

三、高效技巧：学习率范围测试

演示的方法，就是为了解决上述问题。它在一个单次、短暂的实验中，系统性地探索从极小到极大的学习率范围，并观察其对损失的影响，从而快速定位出最佳的学习率区间。

操作步骤 (Step-by-Step)

设定一个学习率的变化范围

我们不测试几个离散的点，而是测试一个连续变化的范围。关键在于，这个范围应该是对数尺度 (log scale) 的，因为我们更关心学习率的数量级（是 0.1 级别还是 0.01 级别）。

在代码中，这通常通过 lrs = 10**torch.linspace(-3, 0, 1000) 实现。
- torch.linspace(-3, 0, 1000): 生成从 -3 到 0 的 1000 个等间距数字。
- 10**...: 将上面的数字作为 10 的指数。
- 结果就是 lrs 包含了从 10**-3 (0.001) 到 10**0 (1.0) 的 1000 个平滑递增的学习率。
进行一个短暂的“预训练”

我们让模型开始训练，但不是用一个固定的学习率，而是在每一次迭代（或每一步）中，都从上面生成的 lrs 列表中按顺序取出一个新的、更大的学习率来更新参数。
- 第1步更新，使用 lr = 0.001
- 第2步更新，使用 lr = 0.001007
- …
- 第1000步更新，使用 lr = 1.0
  
  同时，在每一步，我们都记录下当前使用的学习率和该步计算出的损失值 (loss)。这个过程通常只需要几百或几千次迭代，非常快。
绘制并解读“学习率 vs. 损失”曲线

实验结束后，我们以学习率（X轴，对数坐标）和损失（Y轴）为坐标，将记录下的数据点绘制成图。你会得到一条非常典型的曲线，大致分为四个区域：
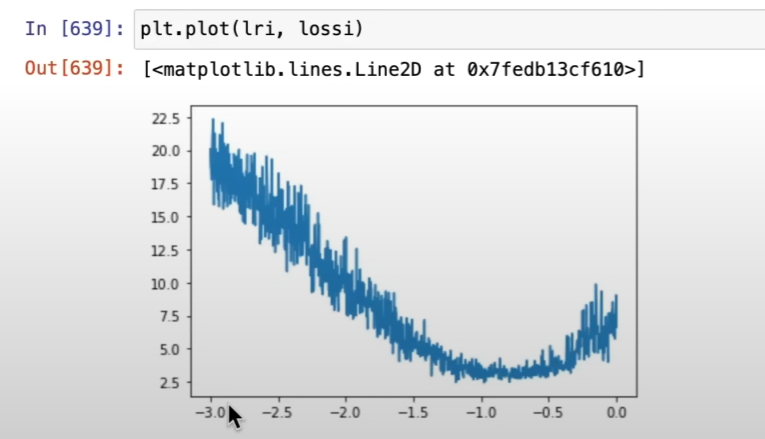
- 区域 A (平坦区)：学习率太小。损失几乎不下降，因为步子太小，模型基本没在学习。
- 区域 B (急降区)：学习率进入了合适的范围。损失开始迅速、稳定地下降。这是我们最感兴趣的区域。
- 区域 C (平原区)：学习率达到了最佳值附近。损失下降到最低点，并可能维持一小段。
- 区域 D (爆炸区)：学习率太大。损失突然开始急剧上升，模型训练开始发散，变得不稳定。

如何选择最佳学习率？

最关键的一步来了。看着这张图，你应该选择哪个值作为你正式训练的学习率呢？

错误的选择：直接选择让损失值最低的那个点（区域C的末端）。
为什么错误：这个点位于“悬崖边上”，是模型能够承受的最大学习率。虽然它在当前这个短暂的实验中让损失下降最快，但在漫长的正式训练中，任何微小的数据波动都可能让它“一步踏空”，直接进入爆炸区，导致训练失败。这个学习率太激进了。
正确且稳妥的选择 (Rule of Thumb)：
1. 找到损失开始爆炸前的最低点所在的学习率（比如图中的 10**-1，即 0.1）。
2. 将这个值除以10。也就是 0.1 / 10 = 0.01（即 10**-2）。
3. 这个 0.01 就是一个非常棒的初始学习率！
这个选择让你处于急降区的中间位置（区域B）。在这个位置，学习率足够大，可以保证损失快速下降（训练速度快），同时又远离“悬崖”，有足够的安全边际来保证整个训练过程的稳定性。

解读loss函数图

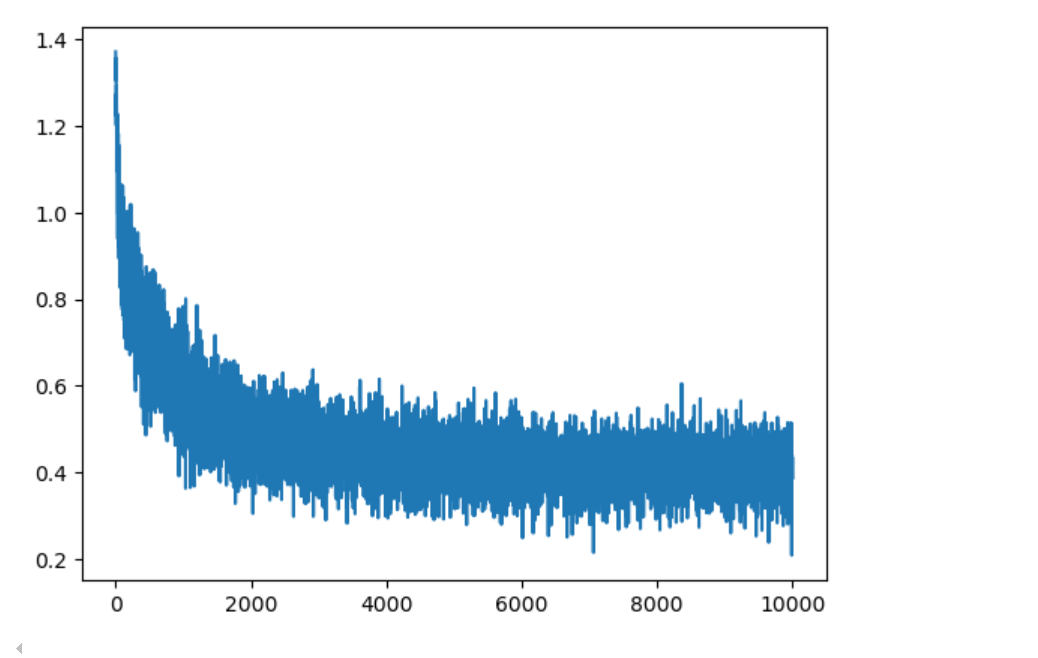
整体训练状态

训练成功的迹象：

明显的下降趋势：损失从约 1.4 快速下降到 0.2 左右
收敛稳定：在后期基本稳定在较低水平
无明显震荡：曲线相对平滑，没有剧烈波动

详细阶段分析

阶段 1：快速下降期 (0-25000 步)

特征：损失急剧下降
含义：模型快速学习基本模式
学习率：0.1（较高），促进快速学习

阶段 2：平缓下降期 (25000-100000 步)

特征：下降速度放缓但持续
含义：模型细化对数据的理解
仍在学习：未完全收敛

阶段 3：稳定收敛期 (100000-200000 步)

特征：损失趋于稳定，小幅震荡
学习率切换：从 0.1 降到 0.01
收敛状态：模型基本训练完成

词嵌入空间

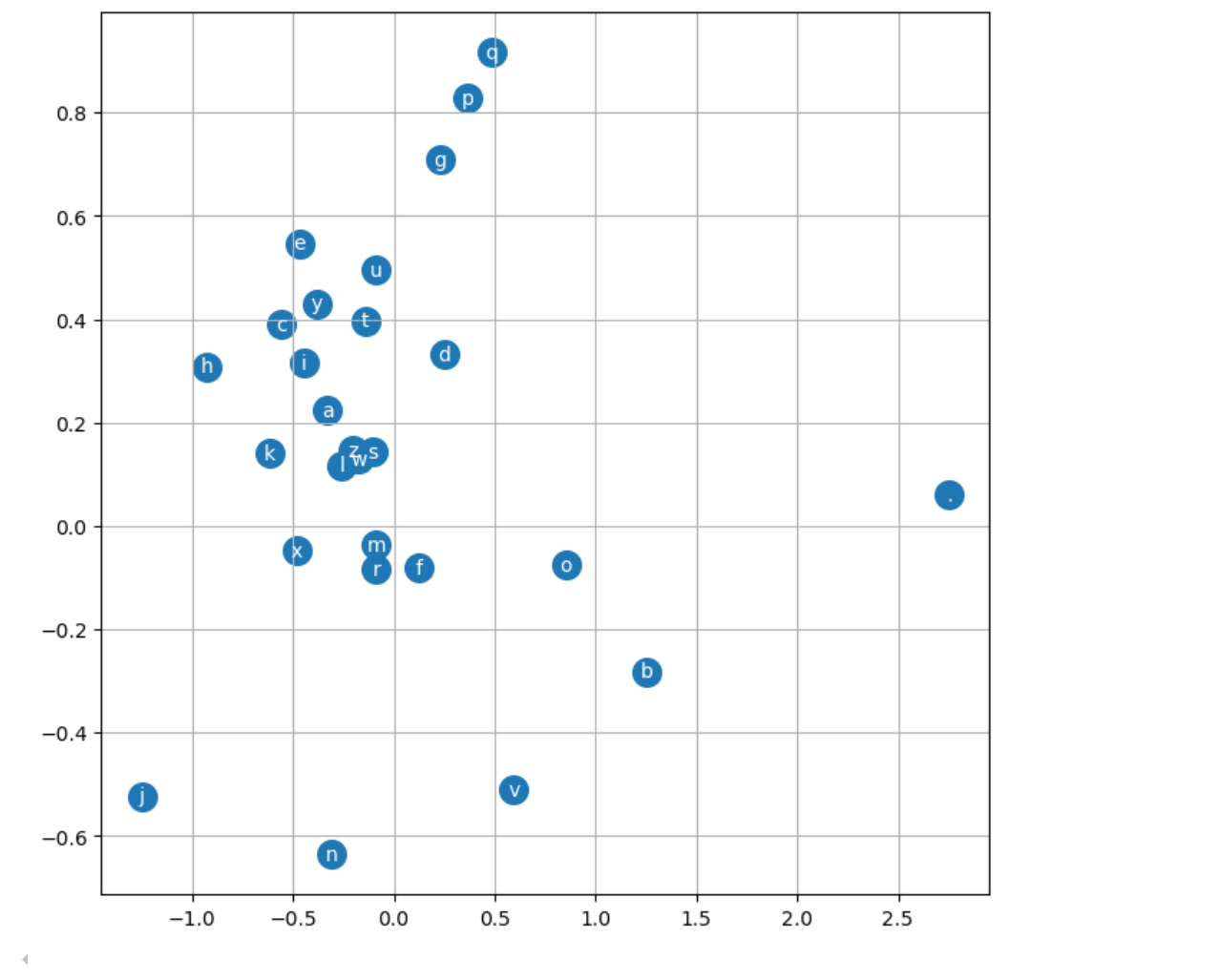
语言学模式发现

1. 元音字母聚类

观察：a, e, i, o, u, y 在图中相对聚集

位置：主要分布在中心区域 (-0.5 到 0.5 范围)
含义：模型自动学习到了元音的相似性
语言学意义：元音在名字中有相似的功能和分布模式

2. 特殊字符的独特位置

结束符 .：

位置：右上角 (约 2.5, 0.05)，远离其他字符
含义：模型学习到结束符的特殊性
功能：标记单词边界，与其他字符有本质不同

3. 辅音字母的分散分布

观察：辅音字母分布更加分散

高频辅音：r, n, l, m 等相对靠近中心
低频辅音：j, q, x, z 等分布在边缘
含义：模型根据使用频率和上下文相似性进行了分组

分类

标签

在 Embedding 里 dim 的意思