Algorithm-Insertion sort, merge sort

算法
1.6k 词

Insertion sort

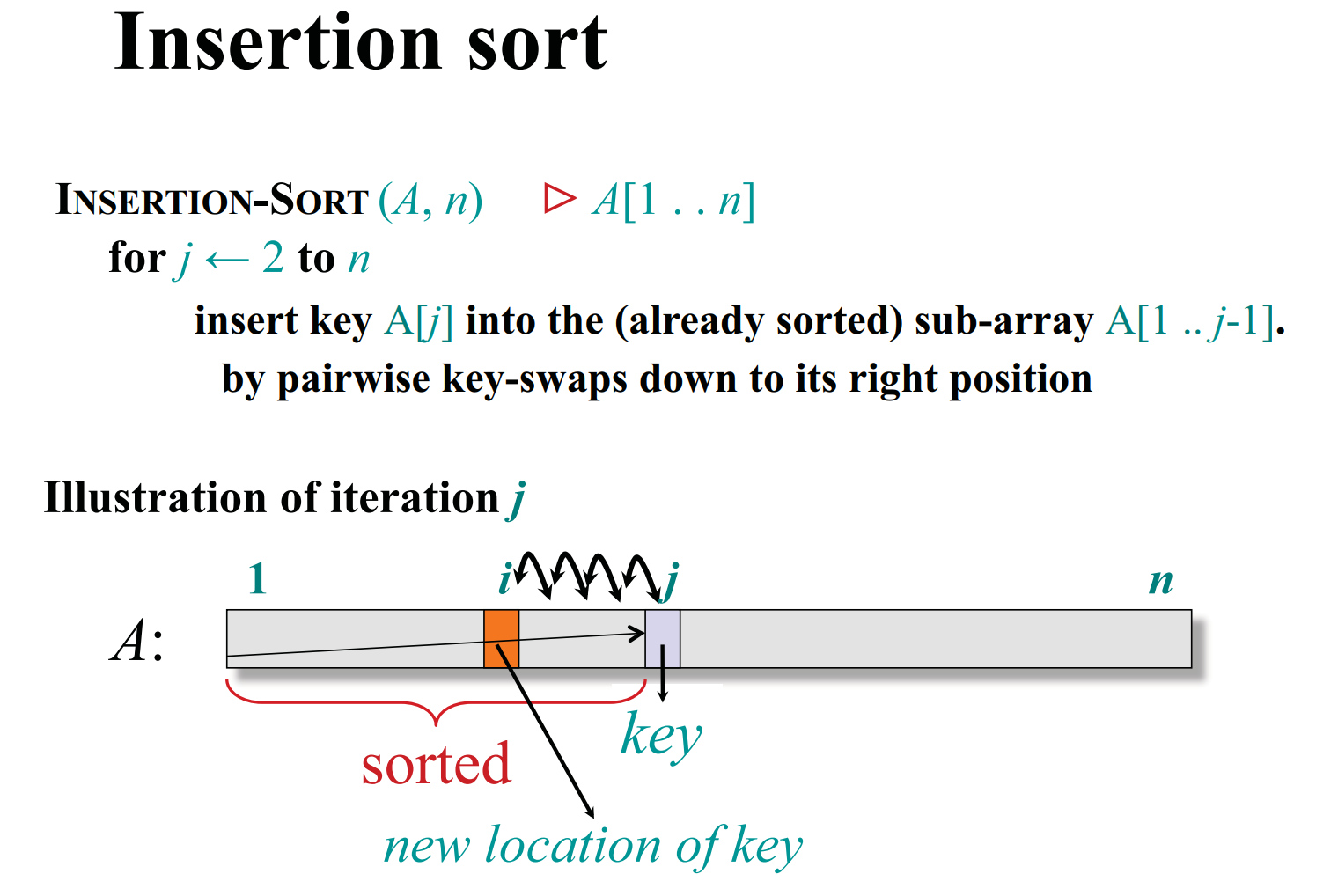
image.png

Example

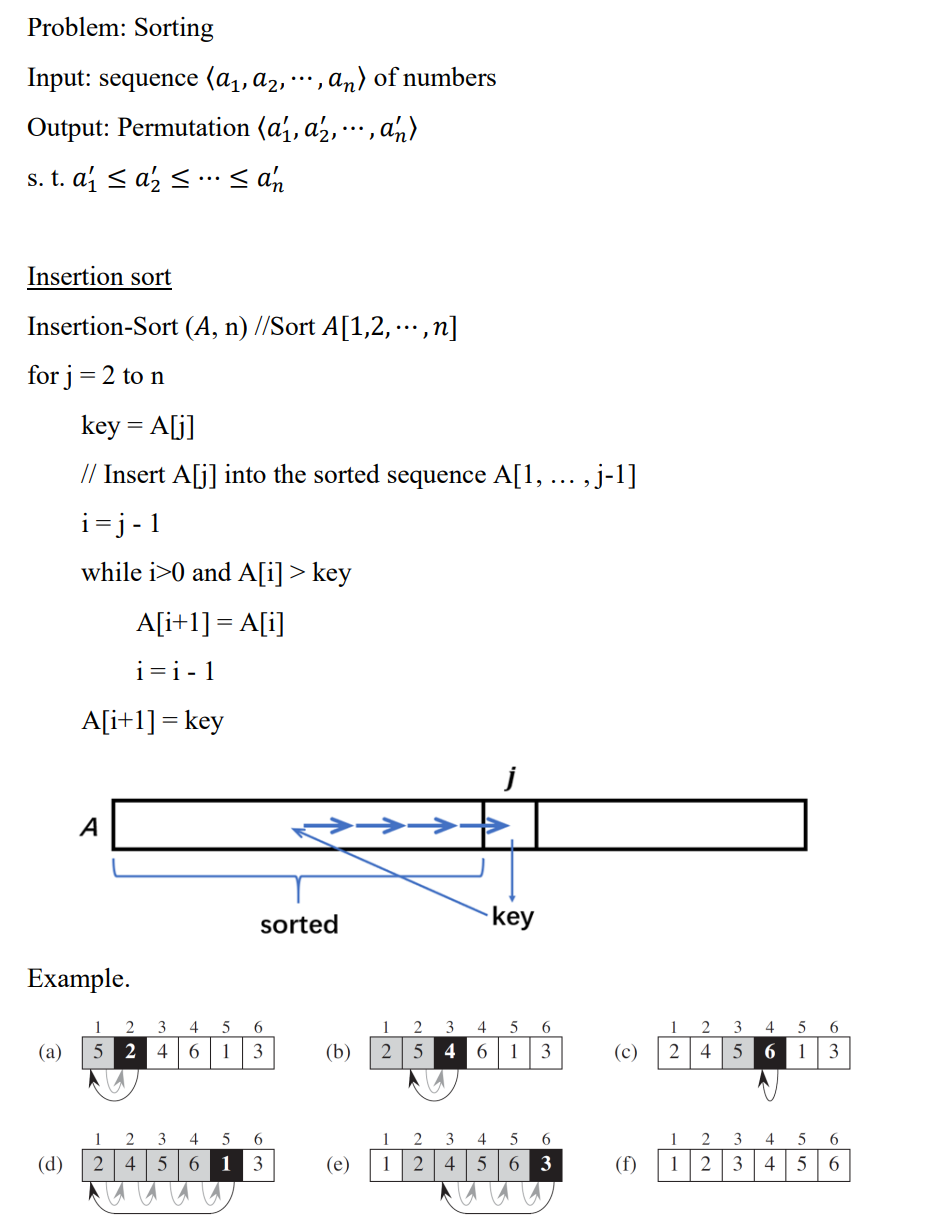
image.png

image.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def insertion_sort (arr):

    n=len(arr)

    for i in range(1,n):

        key=arr[i]

        j=i-1

        while j>=0 and key < arr[j]:

            arr[j+1]=arr[j]

            j-=1
  
        arr[j+1]=key 
        #这里要j+1的原因是，以第一个位置为例：j=0的时候挪到了j=1位置，j就变成-1了
  
    return arr

arr[j+1]=key:
这里要的原因是，以第一个位置为例：的时候挪到了位置，就变成了

时间复杂度

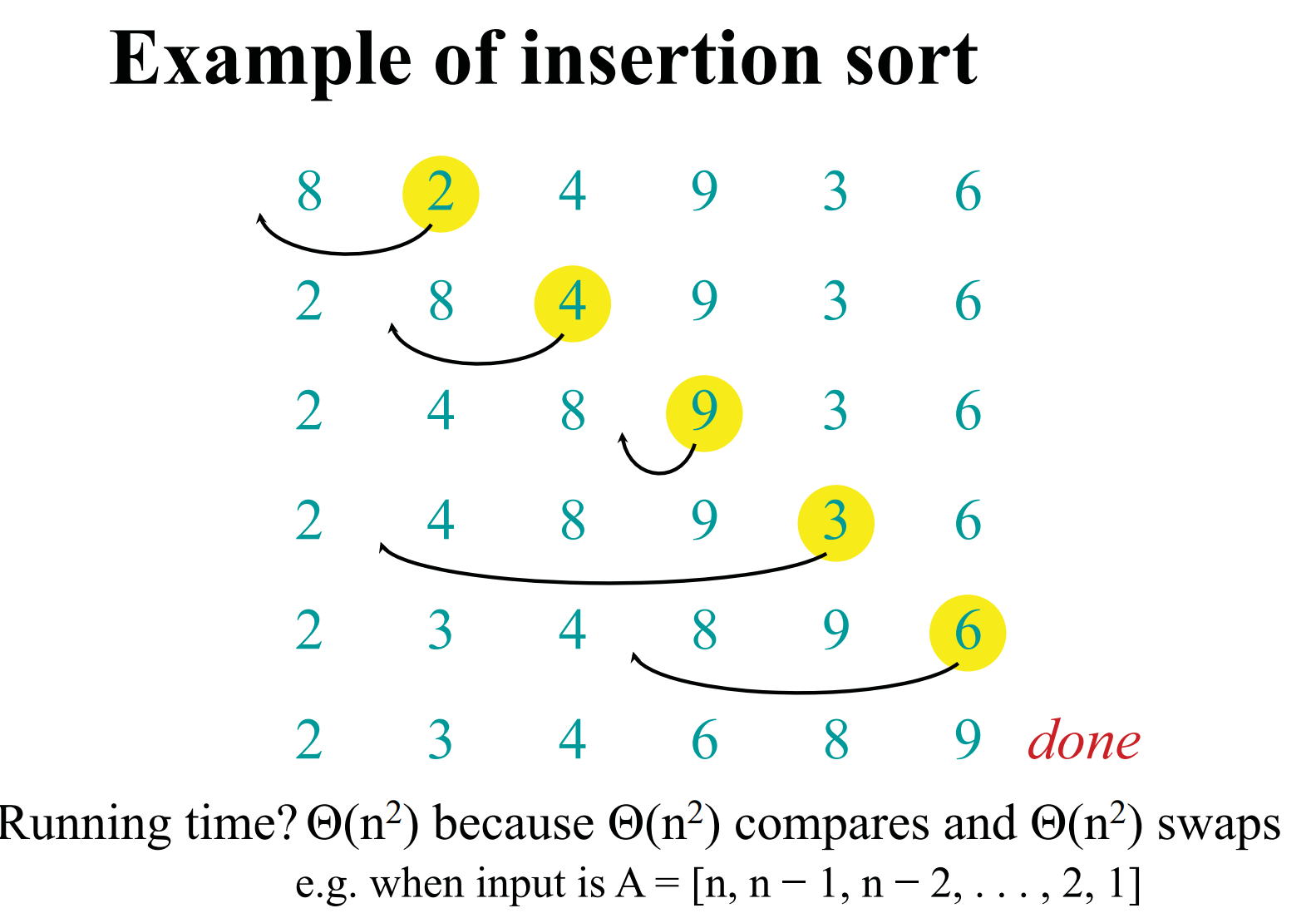
插入排序在最坏情况下（完全逆序输入）时间复杂度

最坏情况：完全逆序

假设数组是 [n, n-1, ..., 2, 1]，那么：

  • 当 i = 1（第 2 个元素），它要和前面 1 个比较、挪动。

  • 当 i = 2（第 3 个元素），要和前面 2 个比较、挪动。

  • 当 i = 3，要和前面 3 个比较、挪动。

  • ……

  • 当 i = n-1（最后一个元素），要和前面 n-1 个全部比较、挪动。

总操作次数

比较/挪动的总次数是：

时间复杂度

  • 这是一个 二次函数量级，即

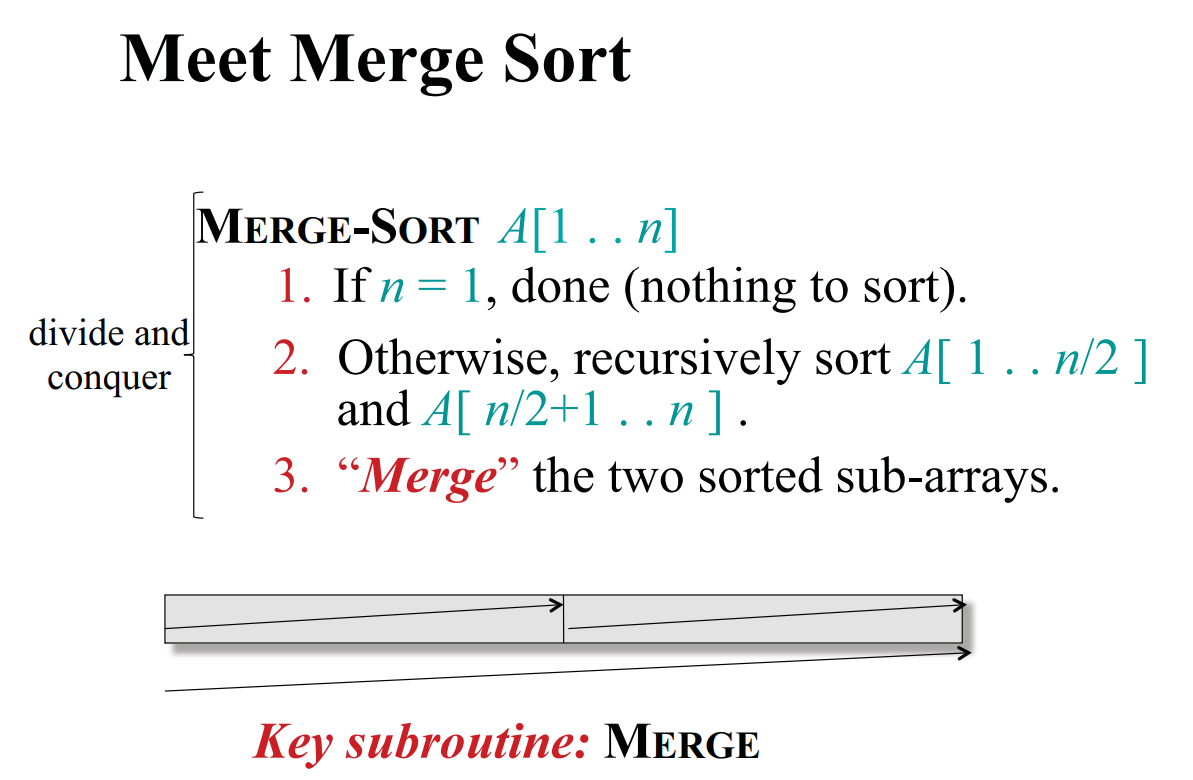
Merge Sort

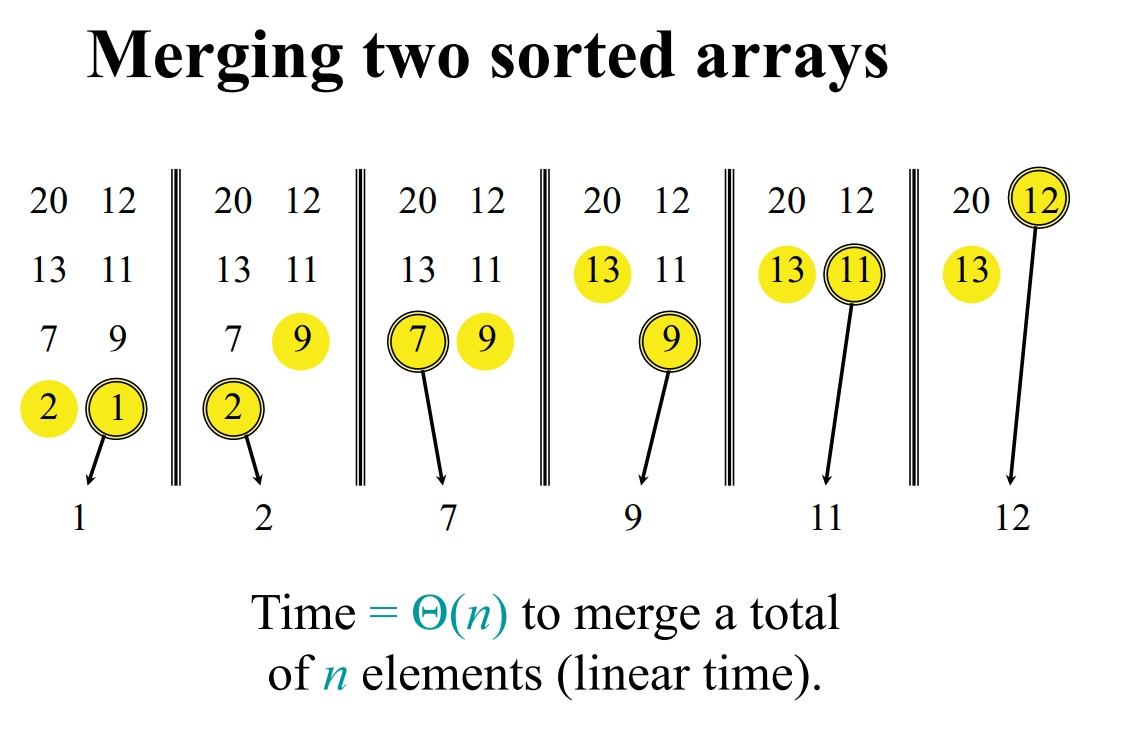
image.png

Example

image.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
def merge_sort(arr,p,q):

    r= (p+q)//2

    if p<q:

        merge_sort(arr,p,r)  # 递归排序左半部分

        merge_sort(arr,r+1,q)  # 递归排序右半部分

        merge(arr,p,q,r)  # 合并两个有序子数组

  
  

def merge(arr,p,q,r):

    n1=r-p+1  # 左子数组长度

    n2=q-r    # 右子数组长度

    L=[0]*n1  # 左子数组

    R=[0]*n2  # 右子数组

    # 复制数据到临时数组

    for i in range(0,n1):

        L[i]=arr[p+i]

  

    for j in range(0,n2):

        R[j]=arr[r+j+1]

  

    # 合并两个有序数组

    i=0

    j=0

    a=p

    while i < n1 and j<n2:

        if L[i] <= R[j]:

            arr[a]=L[i]

            i+=1

        else:

            arr[a]=R[j]

            j+=1

        a+=1

  

    # 复制剩余元素

    while j<n2:

        arr[a]=R[j]

        a+=1

        j+=1

    while i<n1:

        arr[a]=L[i]

        a+=1

        i+=1

  

    return arr

递归树角度理解

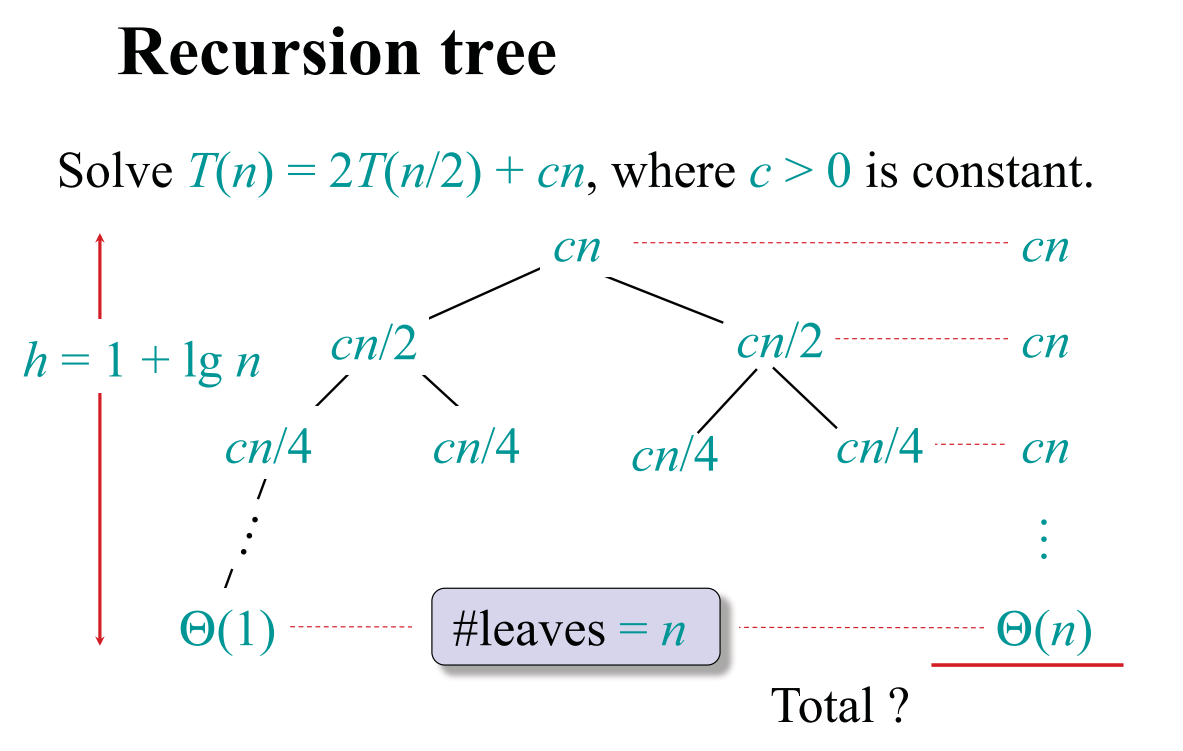
image.png

的来源

每次递归规模减半

归并排序的递归过程：

  • 第 0 层：规模

  • 第 1 层：规模

  • 第 2 层：规模

  • 第 3 层：规模

  • …

  • 第 kk 层：规模

停止条件

递归什么时候停？

  • 当子问题规模 = 1 时，排序自然完成，不再继续递归。

  • 所以停止条件是

leaves（叶子结点）

什么是叶子结点

  • 递归树的 叶子结点 指的是递归停止的地方。

  • 在归并排序中，递归停止条件是 子数组规模 = 1（一个数本身就是有序的）。

  • 所以叶子结点对应 规模为 1 的子问题。

叶子数量是多少

  • 一开始我们有 n个元素。

  • 递归分解到底，每个元素单独成为一个“子数组”。

  • 所以叶子结点的数量就是 n。

补充两种排序方式选择排序和冒泡排序：

image.png