Hypothesis testing and Least squares prediction

数学
1.7k 词

Hypothesis testing on a single parameter

t-test(查表）

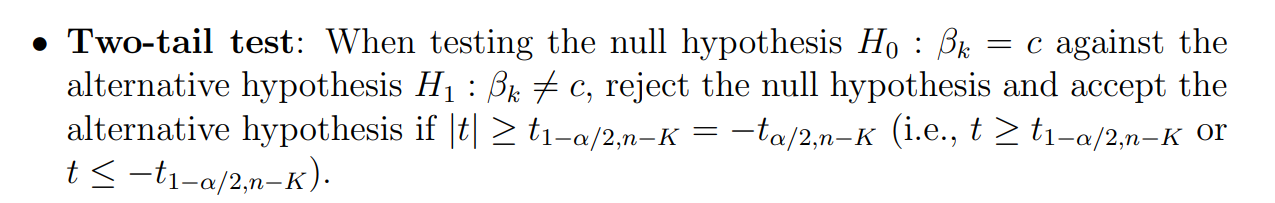
image.png

image.png

补充说明：

significant leve = Prob(type I error)

In hypothesis testing, the significance level is defined as the probability of committing a Type I error, i.e., rejecting the null hypothesiswhen it is in fact true. In other words, represents the maximum risk of a false positive that the researcher is willing to tolerate.

Rejection region（拒绝域）

  • 拒绝域 = 在原假设为真时，观测到的检验统计量落入极端区域（尾部）的区间。
  • “极端”是相对于 备择假设所描述的方向 来定义的。

In short, the sign and form of the alternative hypothesis specify which outcomes are “extreme” or “unlikely under ,” and that in turn dictates whether the rejection region is in the left tail, right tail, or both tails.

p-value approach

image.png

Hypothesis testing on a linear combination of parameters

image.png

Least squares prediction

image.png
image.png

参数估计的无偏性 (Unbiased Estimation)

  • 对象：回归系数 。

  • 定义：估计量的期望等于真实参数。

  • 意义：在重复抽样下，OLS 得到的系数估计在平均意义上是正确的，不会系统性偏大或偏小。

预测的无偏性 (Unbiased Prediction)

  • 对象：预测值 与真实条件期望 。

  • 定义：预测量的期望等于真实的条件均值。

  • 意义：在平均意义上，预测值不会系统性偏离真实均值。

  • 等价说法：预测误差 满足

预测区间是什么

  • 在回归中，我们不光要给出一个预测点 ，还要回答：真实的新观测值有多大概率落在哪个区间？

  • 这个区间就是 预测区间（Prediction Interval, PI）。

  • 数学形式：

    $$PI: \quad \hat{y}0 \ \pm \ t{1-\alpha/2, , n-k-1} \cdot se(f)$$

    其中 se(f)是预测误差的标准误。

PI说明了什么

  • 预测区间包含了两部分不确定性：

    1. 模型估计的不确定性（参数估计方差带来的影响）。

    2. 随机误差本身（每个新观测值都带有）。

  • 因此，预测区间 比均值响应的置信区间更宽。

    • Confidence Interval (CI): 针对 。

    • Prediction Interval (PI): 针对单个新点 Y0Y_0。

95% CI 回顾

  • CI 针对的是 总体参数/均值响应。

  • 含义：如果我们不断重复抽样、建模并计算置信区间，那么其中大约 95% 的区间会覆盖真实的平均响应 。

  • 关注的是 均值。

95% PI 的定义

  • PI 针对的是 未来单个观测值 。

  • 数学表达：

    $$P\Big( \hat{y}0 - t{0.975,n-k-1} \cdot se(f) \ \le Y_0 \le \ \hat{y}0 + t{0.975,n-k-1} \cdot se(f) \Big) \approx 0.95$$

  • 含义：在固定 的情况下，未来新观测 落在区间里的概率大约是 95%。

  • 关注的是 单个点。